Cho hình phẳng \(D\) giới hạn bởi đường cong \(y = \sqrt {2 + \cos x} ,\) trục hoành và các đường thẳng \(x = 0,x = \frac{\pi }{2}\). Khối tròn xoay tạo thành khi \(D\) quay quanh trục hoành có thể tích \(V\) bằng bao nhiêu?
A. \(V = (\pi + 1)\pi \)
B. \(V = \pi - 1\)
C. \(V = \pi + 1\)
D. \(V = (\pi - 1)\pi \)
Quảng cáo
Trả lời:
Chọn A
\(V = \pi \int\limits_0^{\frac{\pi }{2}} {{{\left( {\sqrt {2 + \cos x} } \right)}^2}dx = \left. {\pi \left( {2x + \sin x} \right)} \right|_0^{\frac{\pi }{2}} = \pi } (\pi + 1).\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(V = 156\)
B. \(V = 156\pi \)
C. \(V = 312\)
D. \(V = 312\pi \)
Lời giải
Chọn A
Diện tích thiết diện là: \(S(x) = 3x.\left( {3{x^2} - 2} \right) = 9{x^3} - 6x\)
\( \Rightarrow \) Thể tích vật thể là: \(V = \int\limits_1^3 {\left( {9{x^3} - 6x} \right)dx = 156} \)
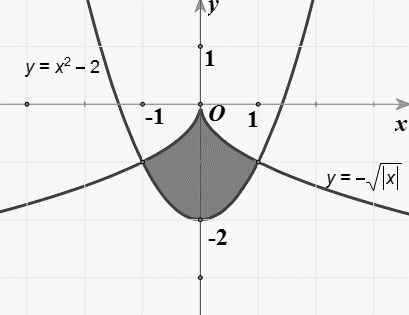
Câu 2
A. \[\int\limits_{ - 1}^1 {\left( {{x^2} - 2 + \sqrt {\left| x \right|} } \right){\rm{d}}x} \].
B. \[\int\limits_{ - 1}^1 {\left( {{x^2} - 2 - \sqrt {\left| x \right|} } \right){\rm{d}}x} \].
C. \[\int\limits_{ - 1}^1 {\left( { - {x^2} + 2 + \sqrt {\left| x \right|} } \right){\rm{d}}x} \].
D. \[\int\limits_{ - 1}^1 {\left( { - {x^2} + 2 - \sqrt {\left| x \right|} } \right){\rm{d}}x} \].
Lời giải
Chọn D
Diện tích hình phẳng được tô đậm trong hình vẽ bên là:
\[\int\limits_{ - 1}^1 {\left| {{x^2} - 2 - \left( { - \sqrt {\left| x \right|} } \right)} \right|{\rm{d}}x} = \int\limits_{ - 1}^1 {\left( { - \sqrt {\left| x \right|} - {x^2} + 2} \right){\rm{d}}x} \] ( vì \(x \in \left[ { - 1;1} \right] \Rightarrow - \sqrt {\left| x \right|} > {x^2} - 2\)).
Câu 3
A. \(\frac{4}{3}\)
B. \(\frac{7}{3}\)
C. \(\frac{8}{3}\)
D. \(\frac{5}{3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
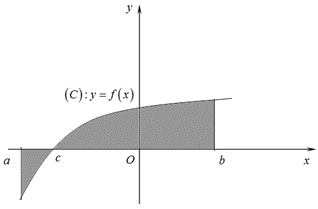
Câu 4
A. \(S = \int\limits_a^c {f\left( x \right){\rm{d}}x + \int\limits_c^b {f\left( x \right){\rm{d}}x} } \).
B. \[S = \int\limits_a^b {f\left( x \right){\rm{d}}x} \].
C. \(S = - \int\limits_a^c {f\left( x \right){\rm{d}}x + \int\limits_c^b {f\left( x \right){\rm{d}}x} } \).
D. \[S = \left| {\int\limits_a^b {f\left( x \right){\rm{d}}x} } \right|\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[S = \frac{{2000}}{3}\].
B. \(S = 2008\).
C. \[S = 2000\].
D. \(S = \frac{{2008}}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \({S_D} = \int\limits_a^0 {f\left( x \right){\rm{d}}x} + \int\limits_0^b {f\left( x \right){\rm{d}}x} \).
B. \({S_D} = - \int\limits_a^0 {f\left( x \right){\rm{d}}x} + \int\limits_0^b {f\left( x \right){\rm{d}}x} \).
C. \({S_D} = \int\limits_a^0 {f\left( x \right){\rm{d}}x} - \int\limits_0^b {f\left( x \right){\rm{d}}x} \).
D. \({S_D} = - \int\limits_a^0 {f\left( x \right){\rm{d}}x} - \int\limits_0^b {f\left( x \right){\rm{d}}x} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(4\).
B. \(\frac{{20}}{3}\).
C. \(\frac{4}{3}\).
D. \(\frac{{16}}{3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số y = f( x ) liên tục trên đoạn [a;b]. Gọi [D] là diện tích hình phẳng giới hạn bởi đồ thị ( C):y = f( x ), trục hoành, (ảnh 1)](https://video.vietjack.com/upload2/images/1753777506/1753777575-image3.png)