Cho phương trình \(\sqrt {2{x^2} + 5} = \sqrt {{x^2} - x + 11} \) (*).
a) Điều kiện: \(x \ge 0\).
b) Bình phương hai vế của phương trình (*) ta được \({x^2} + x - 6 = 0\).
c) Phương trình (*) có 1 nghiệm.
d) Giả sử \({x_1},{x_2}\,\left( {{x_1} < {x_2}} \right)\) là nghiệm của phương trình (*) khi đó: \({x_1} - 2{x_2} = 7\).
Quảng cáo
Trả lời:
Lời giải
a) Sai. Điều kiện của phương trình là \(\left\{ \begin{array}{l}2{x^2} + 5 \ge 0\\{x^2} - x + 11 \ge 0\end{array} \right.\), điều này luôn đúng với mọi \(x \in \mathbb{R}\).
b) Đúng. Bình phương hai vế phương trình (*), ta được: \(2{x^2} + 5 = {x^2} - x + 11\).
Rút gọn ta được \({x^2} + x - 6 = 0\).
c) Sai. Phương trình \({x^2} + x - 6 = 0\) có hai nghiệm \(x = 2\); \(x = - 3\).
Thay giá trị \(x = 2\) vào phương trình (*): \(\sqrt {13} = \sqrt {13} \) (thỏa mãn).
Thay giá trị \(x = - 3\) vào phương trình (*): \(\sqrt {23} = \sqrt {23} \) (thỏa mãn).
Vậy tập nghiệm phương trình là \(S = \left\{ {2; - 3} \right\}\).
d) Sai. Với \({x_1},{x_2}\,\left( {{x_1} < {x_2}} \right)\) là nghiệm của phương trình (*), ta có \({x_1} = - 3;{x_2} = 2\).
Khi đó, \({x_1} - 2{x_2} = - 3 - 2 \cdot 2 = - 7\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
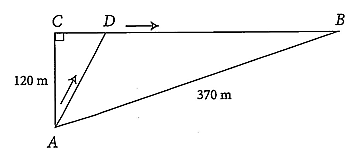
Gọi thời gian chú thỏ chạy trên đoạn \(AD\) là \(x\,\,\left( {0 < x < 30} \right)\) (giây), khi đó thời gian chú thỏ chạy trên đoạn \(BD\) là \(30 - x\) (giây). Do đó, quãng đường \(AD\) và \(BD\) lần lượt là \(13x\,\,{\rm{(m)}}\) và \(15\left( {30 - x} \right)\,\,{\rm{(m)}}\).
Độ dài quãng đường \(BC\) là: \(\sqrt {{{370}^2} - {{120}^2}} = 350\,\,{\rm{(m)}}\).
Tam giác \(ACD\) vuông tại \(C\) nên \(CD = \sqrt {{{\left( {13x} \right)}^2} - {{120}^2}} \,\,{\rm{(m)}}\).
Mặt khác, \(CD = BC - BD = 350 - 15\left( {30 - x} \right)\,\,{\rm{(m)}}\).
Do đó, ta có: \(\sqrt {{{\left( {13x} \right)}^2} - {{120}^2}} = 350 - 15\left( {30 - x} \right)\).
Giải phương trình này và kết hợp với điều kiện \(0 < x < 30\), ta nhận \(x = 10\) (giây).
Vậy khoảng cách giữa vị trí \(C\) và vị trí \(D\) là: \(350 - 15 \cdot \left( {30 - 10} \right) = 50\,\,{\rm{(m)}}\).
Đáp án: \(50\).
Lời giải
Lời giải
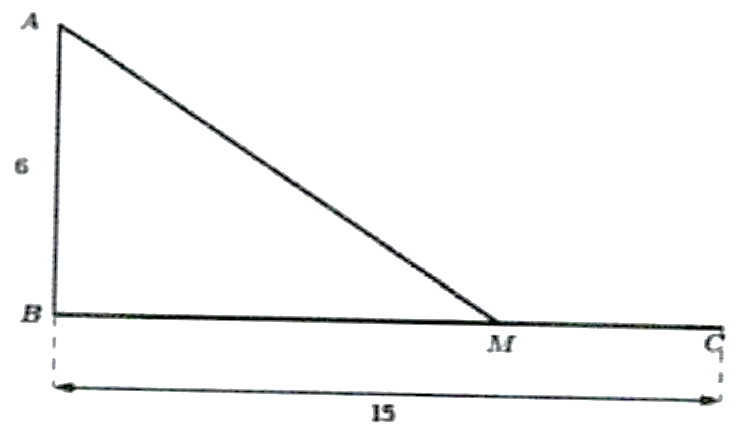
Ta có 1 giờ 14 phút \( = \frac{{37}}{{30}}\) giờ. Gọi \[AM = x\;\,{\rm{(km)}}\,\,\,\left( {x > 6} \right)\].
Suy ra thời gian đi từ \(A\) đến \(M\) là \(\frac{x}{{10}}\) (giờ).
Khi đó \(BM = \sqrt {{x^2} - 36} \) và \(CM = 15 - \sqrt {{x^2} - 36} \).
Thời gian đi từ \(M\) đến \(C\) là \(\frac{{15 - \sqrt {{x^2} - 36} }}{{30}}\).
Theo giả thiết ta có phương trình: \(\frac{x}{{10}} + \frac{{15 - \sqrt {{x^2} - 36} }}{{30}} = \frac{{37}}{{30}}\).
Giải phương trình ta được \(x = 10\,\,{\rm{(km)}}\).
Do đó tổng quảng đường phải đi là \(AM + MC = 10 + \left( {15 - \sqrt {{{10}^2} - 36} } \right) = 17\,\,{\rm{(km)}}\).
Đáp án: 17.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(0\).
B. \(1\).
C. \(2\).
D. \(3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.