Cho hai biến cố \(A\), \(B\) có \({\rm{P}}(A) = 0,5;{\rm{P}}(B) = 0,8;{\rm{P}}(A \cap B) = 0\),4. Tính các xác suất sau: \({\rm{P}}(A\mid B);{\rm{P}}(B\mid A)\).
Cho hai biến cố \(A\), \(B\) có \({\rm{P}}(A) = 0,5;{\rm{P}}(B) = 0,8;{\rm{P}}(A \cap B) = 0\),4. Tính các xác suất sau: \({\rm{P}}(A\mid B);{\rm{P}}(B\mid A)\).
Quảng cáo
Trả lời:
Ta có: \({\rm{P}}(A\mid B) = \frac{{{\rm{P}}(A \cap B)}}{{{\rm{P}}(B)}} = \frac{{0,4}}{{0,8}} = 0,5;{\rm{ P}}(B\mid A) = \frac{{{\rm{P}}(B \cap A)}}{{{\rm{P}}(A)}} = \frac{{0,4}}{{0,5}} = 0,8\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
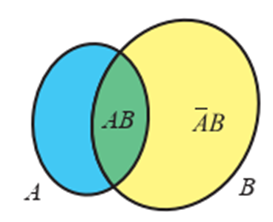
Theo công thức nhân xác suất, ta có \(P(AB) = P(B)P(A\mid B) = 0,2\).
Vì \(\bar AB\) và \(AB\) là hai biến cố xung khắc và \(\bar AB \cup AB = B\) nên theo tính chất của xác suất, ta có \(P(\bar AB) = P(B) - P(AB) = 0,3\).
Theo công thức tính xác suất có điều kiện, \(P(\bar A\mid B) = \frac{{P(\bar AB)}}{{P(B)}} = \frac{{0,3}}{{0,5}} = 0,6.\)
Lời giải
Gọi \(A\) là biến cố "Thành viên được chọn biết chơi cờ tướng" và \(B\) là biến cố "Thành viên được chọn biết chơi cờ vua".
Số thành viên của câu lạc bộ biết chơi cả hai môn cờ là \(20 + 25 - 35 = 10\).
Do đó, trong số 20 thành viên biết chơi cờ tướng, có đúng 10 thành viên biết chơi cờ vua.
Vậy nên xác suất thành viên được chọn biết chơi cờ vua, biết rằng thành viên đó biết chơi cờ tướng là \(P(B\mid A) = \frac{{10}}{{20}} = 0,5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.