Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:
Thu nhập
[5; 8)
[8; 11)
[11; 14)
[14; 17)
[17; 20)
Số người của nhà máy A
20
35
45
35
20
Số người của nhà máy B
17
23
30
23
17
Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.
Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:
|
Thu nhập |
[5; 8) |
[8; 11) |
[11; 14) |
[14; 17) |
[17; 20) |
|
Số người của nhà máy A |
20 |
35 |
45 |
35 |
20 |
|
Số người của nhà máy B |
17 |
23 |
30 |
23 |
17 |
Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.
Câu hỏi trong đề: 19 bài tập Khoảng tứ phân vị (có lời giải) !!
Quảng cáo
Trả lời:
Chọn giá trị đại diện cho mẫu số liệu ta có:
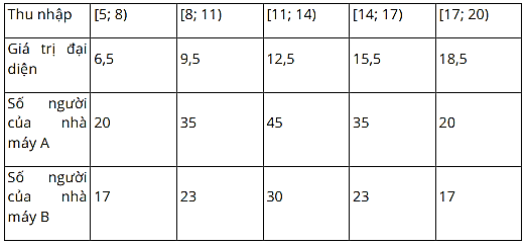
Mức thu nhập trung bình của người lao động nhà máy \({\rm{A}}\) là:
\(\frac{{6,5.20 + 9,5.35 + 12,5.45 + 15,5.35 + 18,5.20}}{{(20 + 35 + 45 + 35 + 20)}} = 12,5{\rm{ (tri?u d?ng)}}{\rm{. }}\)
Mức thu nhập trung bình của người lao động nhà máy \({\rm{B}}\) là:
\(\frac{{6,5.17 + 9,5.23 + 12,5 \cdot 30 + 15,5.23 + 18,5.17}}{{(17 + 23 + 30 + 23 + 17)}} = 12,5{\rm{ (tri?u d?ng)}}{\rm{. }}\)
Nhà máy \({\rm{A}}\)
Cỡ mẫu \(n = 20 + 35 + 45 + 35 + 20 = 155\).
Gọi \({x_1};{x_2}; \ldots ;{x_{155}}\) là mức thu nhập của 155 công nhân lao động của nhà máy \(A\) và được sắp xếp theo thứ tự tăng dần
Tứ phân vị thứ nhất của mẫu số liệu là \({x_{39}}\) thuộc nhóm \([8;11)\) nên nhóm chứa tứ phân vị thứ nhất là \([8;11)\).
Ta có \({Q_1} = 8 + \frac{{\frac{{155}}{4} - 20}}{{35}} \cdot (11 - 8) \approx 9,6\).
Tứ phân vị thứ ba của mẵu số liệu là \({x_{117}}\) thuộc nhóm \([14;17)\) nên nhóm chứa tứ phân vị thứ ba là \([14;17)\).
Ta có \({Q_3} = 14 + \frac{{\frac{{155.3}}{4} - 100}}{{35}} \cdot (17 - 14) \approx 15,4\).
Khoảng tứ phân vị: \({{\rm{R}}_{{\rm{AQ}}}} = 15,4 - 9,6 = 5,8\).
Nhà máy \({\rm{B}}\)
Cơ mẫu \({\rm{n}} = 17 + 23 + 30 + 23 + 17 = 110\).
Gọi \({{\rm{y}}_1};{{\rm{y}}_2}; \ldots ;{{\rm{y}}_{110}}\) là mức thu nhập của 110 công nhân lao động của nhà máy \({\rm{B}}\) và được sắp xếp theo thứ tự tăng dần.
Tứ phân vị thứ nhất của mẫu số liệu là \({{\rm{y}}_{28}}\) thuộc nhóm \([8;11)\) nên nhóm chứa tứ phân vị thứ nhất là \([8;11)\).
Ta có \({Q_1} = 8 + \frac{{\frac{{110}}{4} - 17}}{{23}} \cdot (11 - 8) \approx 9,4\).
Tứ phân vị thứ ba của mẫu số liệu là \({y_{83}}\) thuộc nhóm \([14;17)\) nên nhóm chứa tứ phân vị thứ ba là \([14;17)\).
Ta có \({Q_3} = 14 + \frac{{\frac{{3.10}}{4} - 70}}{{23}} \cdot (17 - 14) \approx 15,6\).
Khoảng tứ phân vị .
Vì \({R_{BQ}} > {R_{AQ}}\) nên mức thu nhập của người lao động ở nhà máy \(B\) biến động nhiều hơn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Cỡ mẫu \(n = 25\)
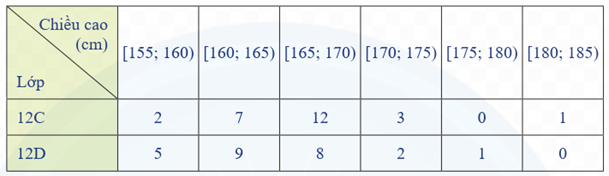
Gọi \({x_1};{x_2}; \ldots ;{x_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp \(12{\rm{C}}\) được xếp theo thứ tự không giảm.
Ta có: \({x_1};{x_2} \in [155;160);{x_3}; \ldots ;{x_9} \in [160;165);{x_{10}}; \ldots ;{x_{21}} \in [165;170);{x_{22}}; \ldots ;{x_{24}} \in [170;175)\); \({x_{25}} \in [180;185)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_6} + {x_7}} \right) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 160 + \frac{{\frac{{25}}{4} - 2}}{7}(165 - 160) = \frac{{4565}}{{28}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 165 + \frac{{\frac{{3.25}}{4} - (2 + 7)}}{{12}}(170 - 165) = \frac{{2705}}{{16}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{675}}{{12}}\)
Gọi \({y_1};{y_2}; \ldots ;{y_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp \(12{\rm{D}}\) được xếp theo thứ tự không giảm.
та có: \({y_1};{y_2}; \ldots ;{y_5} \in [155;160);{y_6}; \ldots ;{y_{14}} \in [160;165);{y_{15}}; \ldots ;{y_{22}} \in [165;170)\);
\({y_{23}};{{\rm{y}}_{24}} \in [170;175);{y_{25}} \in [175;180)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{y_6} + {y_7}} \right) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \(Q_1^\prime = 160 + \frac{{\frac{{25}}{4} - 5}}{9}(165 - 160) = \frac{{5785}}{{36}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}^\prime = 165 + \frac{{\frac{{3.25}}{4} - (5 + 9)}}{8}(170 - 165) = \frac{{5375}}{{32}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}^\prime = {Q_3}^\prime - {Q_1}^\prime = \frac{{2095}}{{288}}\)
Có \({\Delta _Q}^\prime > {\Delta _Q}\) nên chiều cao của các bạn học sinh nữ lớp \(12{\rm{D}}\) có độ phân tán lơn hơn lớp \(12{\rm{C}}\)
Lời giải
Lớp 12A
Khoảng biến thiên: \({{\rm{R}}_1} = 175 - 145 = 30\).
Cơ mẫu \({\rm{n}} = 1 + 0 + 15 + 12 + 10 + 5 = 43\).
Gọi \({{\rm{x}}_1};{{\rm{x}}_2}; \ldots ;{{\rm{x}}_{43}}\) là chiều cao của 43 học sinh lớp \(12\;{\rm{A}}\) được sắp xếp theo thứ tự tăng dần.
Tứ phân vị thứ nhất của mẫu số liệu là \({{\rm{x}}_{11}}\) thuộc nhóm \([155;160)\) nên nhóm chứa tứ phân vị thứ nhất là \([155;160)\).
Ta có \({Q_1} = 155 + \frac{{\frac{{43}}{4} - 1}}{{15}} \cdot (160 - 155) = 158,25\).
Tứ phân vị thứ ba của mẫu số liệu là x33 thuộc nhóm \([165;170)\) nên nhóm chứa tứ phân vị thứ ba là \([165;170)\).
Ta có \({Q_3} = 165 + \frac{{\frac{{43,3}}{4} - 28}}{{10}} \cdot (170 - 165) = 167,125\).
Khoảng tứ phân vị là \({{\rm{D}}_{{\rm{1Q}}}} = 167,125 - 158,25 = 8,875\).
Lớp 12B
Khoảng biến thiên: \({R_2} = 175 - 155 = 20\).
Cỏ mẫu \(n = 17 + 10 + 9 + 6 = 42\).
Gọi \({{\rm{y}}_1};{{\rm{y}}_2}; \ldots ;{{\rm{y}}_{42}}\) là chiều cao của 42 học sinh lớp \(12\;{\rm{B}}\) và được sắp xếp theo thứ tự tăng dần.
Tứ phân vị thứ nhất của mẫu số liệu là \({y_{11}}\) thuộc nhóm \([155;160)\) nên nhóm chứa tứ phân vị thứ nhất là \([155;160)\).
Ta có \({Q_1} = 155 + \frac{{\frac{{42}}{4} - 0}}{{17}} \cdot (160 - 155) \approx 158,1\).
Tứ phân vị thứ ba của mẫu số liệu là \({{\rm{y}}_{32}}\) thuộc nhóm [165;170) nên nhóm chứa tứ phân vị thứ ba là \([165;170)\).
Ta có \({Q_2} = 165 + \frac{{\frac{{423}}{4} - 27}}{9} \cdot (170 - 165) = 167,5\).
Khoảng tứ phân vị là: \({R_{2Q}} = 167,5 - 158,1 = 9,4\).
b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này, ta nên dùng khoảng tứ phân vị vì khoảng tứ phân vị chỉ phụ thuộc vào nửa giửa của mẫu số liệu, không bị ảnh hưởng bởi các giá trị bất thường.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.