19 bài tập Khoảng tứ phân vị (có lời giải)
29 người thi tuần này 4.6 269 lượt thi 19 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Lời giải
Cỡ mẫu \(n = 25\)
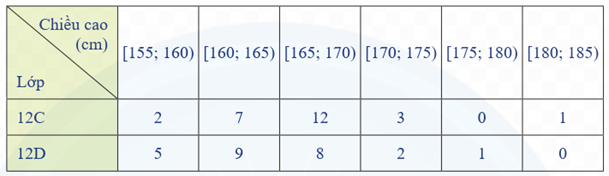
Gọi \({x_1};{x_2}; \ldots ;{x_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp \(12{\rm{C}}\) được xếp theo thứ tự không giảm.
Ta có: \({x_1};{x_2} \in [155;160);{x_3}; \ldots ;{x_9} \in [160;165);{x_{10}}; \ldots ;{x_{21}} \in [165;170);{x_{22}}; \ldots ;{x_{24}} \in [170;175)\); \({x_{25}} \in [180;185)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_6} + {x_7}} \right) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 160 + \frac{{\frac{{25}}{4} - 2}}{7}(165 - 160) = \frac{{4565}}{{28}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 165 + \frac{{\frac{{3.25}}{4} - (2 + 7)}}{{12}}(170 - 165) = \frac{{2705}}{{16}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{675}}{{12}}\)
Gọi \({y_1};{y_2}; \ldots ;{y_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp \(12{\rm{D}}\) được xếp theo thứ tự không giảm.
та có: \({y_1};{y_2}; \ldots ;{y_5} \in [155;160);{y_6}; \ldots ;{y_{14}} \in [160;165);{y_{15}}; \ldots ;{y_{22}} \in [165;170)\);
\({y_{23}};{{\rm{y}}_{24}} \in [170;175);{y_{25}} \in [175;180)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{y_6} + {y_7}} \right) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \(Q_1^\prime = 160 + \frac{{\frac{{25}}{4} - 5}}{9}(165 - 160) = \frac{{5785}}{{36}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}^\prime = 165 + \frac{{\frac{{3.25}}{4} - (5 + 9)}}{8}(170 - 165) = \frac{{5375}}{{32}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}^\prime = {Q_3}^\prime - {Q_1}^\prime = \frac{{2095}}{{288}}\)
Có \({\Delta _Q}^\prime > {\Delta _Q}\) nên chiều cao của các bạn học sinh nữ lớp \(12{\rm{D}}\) có độ phân tán lơn hơn lớp \(12{\rm{C}}\)
Lời giải
c) Gọi \({x_1};{x_2}; \ldots ;{x_{100}}\) là mẫu số liệu gốc gồm thời gian 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan được xếp theo thứ tự không giảm.
Khoảng biến thiên \(R = 33 - 15 = 18\) (phút)
Tа có: \({x_1};{x_2}; \ldots ;{x_{22}} \in [15;18);{x_{23}}; \ldots ;{x_{60}} \in [18;21);{x_{61}}; \ldots ;{x_{87}} \in [21;24)\);
\({x_{88}}; \ldots ;{x_{95}} \in [24;27);{x_{96}}; \ldots ;{x_{99}} \in [27;30);{x_{100}} \in [30;33)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{25}} + {x_{26}}} \right) \in [18;21)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 18 + \frac{{\frac{{100}}{4} - 22}}{{38}}(21 - 18) = \frac{{693}}{{38}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{75}} + {x_{76}}} \right) \in [21;24)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 21 + \frac{{\frac{{3.100}}{4} - (22 + 38)}}{{27}}(24 - 21) = \frac{{68}}{3}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{505}}{{114}}\)
Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu \(x > {Q_3} + 1,5{\Delta _Q}\) hoặc \(x < {Q_1} - 1,5{\Delta _Q}\)
Hay \(x > \frac{{39}}{2} + 1,5 \cdot \frac{{24}}{{19}} = 21,39\) hoă̆c \(x < \frac{{693}}{{38}} - 1,5 \cdot \frac{{24}}{{19}} = 16,34\)
Vậy các giá trị ngoại lệ thuộc khoảng \([15;18);[24;27);[27;30);[30;33)\)
Khoảng biến thiên của mẵu số liệu ghép nhóm sau khi loại bỏ giá trị ngoại lệ: 24 - \(18 = 6\) (phút)
Gọi \({z_1};{z_2}; \ldots ;{z_{65}}\) là mẫu số liệu gốc gồm thời gian 65 lần ông Thắng đi xe buýt từ nhà đến cơ quan được xếp theo thứ tự không giảm, sau khi đā loại bỏ các giá trị ngoại lệ
Ta có: \({z_1};{z_2}; \ldots ,{z_{38}} \in [18;21);{z_{30}}; \ldots ;{x_{65}} \in [21;24)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({z_{17}} \in [18;21)\). Do đó, tứ phân vị thứ nhất của mẵu sô liệu ghép nhóm là: \({Q_1}^{\prime \prime } = 18 + \frac{{\frac{{65}}{4}}}{{38}}(21 - 18) = \frac{{2931}}{{152}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({z_{50}} \in [21;24)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}^{\prime \prime } = 21 + \frac{{\frac{{3.65}}{4} - 38}}{{27}}(24 - 21) = \frac{{799}}{{36}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}^{\prime \prime } = {Q_3}^{\prime \prime } - {Q_1}^{\prime \prime } = 2,91\)
Nhận xét: Sau khi loại bỏ giá trị ngoại lệ, khoảng biến thiên mới giảm mạnh còn khoảng tứ phân vị mới không bị ảnh hường nhiểu
Câu 4
Kết quả điều tra tổng thu nhập trong năm 2022 của một số hộ gia đình trong một địa phương được ghi lại ở bảng sau:
|
Tổng thu nhập (triệu đồng) |
[200; 250) |
[250; 300) |
[300; 350) |
[350; 400) |
[400; 450) |
|
Số hộ gia đình |
24 |
62 |
34 |
21 |
9 |
a) Hãy tìm các tứ phân vị Q1 và Q3.
b) Một doanh nghiệp địa phương muốn hướng dịch vụ của mình đến các gia đình có mức thu nhập ở tầm trung, tức là 50% các hộ gia đình có mức thu nhập ở chính giữa so với tất cả các hộ gia đình của địa phương. Hỏi doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng nào?
Lời giải
a) Cỡ mẫu \(n = 150\)
Gọi \({x_1};{x_2}; \ldots ;{x_{150}}\) là mẫu số liệu gốc gồm thu nhập của 150 hộ gia đình được xếp theo thứ tự không giảm.
та có: \({x_1};{x_2}; \ldots ;{x_{24}} \in [200;250);{x_{25}}; \ldots ;{x_{86}} \in [250;300);{x_{87}}; \ldots ;{x_{120}} \in [300;350)\);
\({x_{121}}; \ldots ;{x_{141}} \in [350;400);{x_{142}}; \ldots ;{x_{150}} \in [400;450)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{38}} \in [250;300)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 250 + \frac{{\frac{{150}}{4} - 24}}{{62}}(300 - 250) = \frac{{16175}}{{62}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{113}} \in [300;350)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 300 + \frac{{\frac{{3.150}}{4} - (24 + 62)}}{{34}}(350 - 300) = \frac{{11525}}{{34}}\)
b) Doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng \(\left[ {{Q_1};{Q_3}} \right) = [260,89;338,97)\) (triệu đồng)
Lời giải
Cỡ mẫu \(n = 30\);
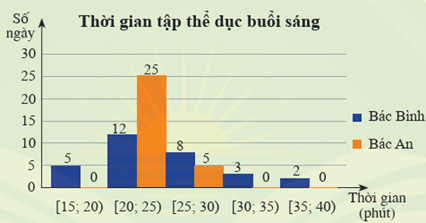
Gọi \({x_1};{x_2}; \ldots ;{x_{30}}\) là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác An được xếp theo thứ tự không giảm.
Ta có: \({x_1};{x_2}; \ldots ;{x_{25}} \in [20;25);{x_{26}}; \ldots ;{x_{30}} \in [25;30)\);
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 20 + \frac{{\frac{{30}}{4}}}{{25}}(25 - 20) = \frac{{43}}{2}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{23}} \in [20;25)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 20 + \frac{{\frac{{3.30}}{4}}}{{25}}(25 - 20) = \frac{{49}}{2}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 3\)
Gọi \({y_1};{y_2}; \ldots ;{y_{30}}\) là mẫu số liệu gốc về thời gian tập thề dục buổi sáng mỗi ngày của bác Bình được xếp theo thứ tự không giảm.
Ta có: \({y_1};{y_2}; \ldots ;{y_5} \in [15;20);{y_6}; \ldots ;{y_{17}} \in [20;25);{y_{18}}; \ldots ;{y_{25}} \in [25;30);{y_{26}};{y_{27}};{y_{28}} \in [30;35)\); \({y_{29}};{y_{30}} \in [35;40)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({y_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \(Q_1^\prime = 20 + \frac{{\frac{{30}}{4}}}{{12}}(25 - 20) = \frac{{185}}{8}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{23}} \in [25;30)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}^\prime = 25 + \frac{{\frac{{3.00}}{4} - (5 + 12)}}{8}(30 - 25) = \frac{{455}}{{16}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}^\prime = {Q_3}^\prime - {Q_1}^\prime = \frac{{85}}{{16}}\)
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình lớn hơn bác An
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.