Câu hỏi:
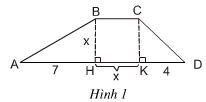
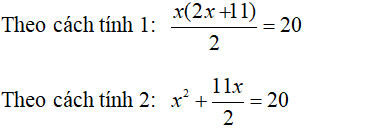13/07/2024 4,068Tính diện tích S của hình thang ABCD theo x bằng hai cách:
1) Tính theo công thức: S = BH x (BC + DA) : 2
2) S = SABH + SBCKH + SCKD
Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?
Câu hỏi trong đề: Giải toán 8: Chương 3: Phương Trình Bậc Nhất Một Ẩn !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Ta có: S = BH x (BC + DA) : 2
+ BCKH là hình chữ nhật nên BC = KH = x
+ BH = x
+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.
Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2 = x.(2x + 11) : 2.
2) S = SABH + SBCKH + SCKD
+ ABH là tam giác vuông tại H
⇒ SBAH = 1/2.BH.AH = 1/2.7.x = 7x/2.
+ BCKH là hình chữ nhật
⇒ SBCKH = x.x = x2.
+ CKD là tam giác vuông tại K
⇒ SCKD = 1/2.CK.KD = 1/2.4.x = 2x.
Do đó: S = SABH + SBCKH + SCKD = 7x/2 + x2 + 2x = x2 + 11x/2.
- Với S = 20 ta có phương trình:
Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
7 – 3x = 9 – x
⇔ 7 – 9 = 3x – x
⇔ -2 = 2x
⇔ -2 : 2 = x
⇔ -1 = x
⇔ x = -1
Vậy phương trình có nghiệm duy nhất x = -1.
Lời giải
x – 5 = 3 – x
⇔ x + x = 5 + 3
⇔ 2x = 8
⇔ x = 8 : 2
⇔ x = 4
Vậy phương trình có nghiệm duy nhất x = 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án