Anh \(X\) nhận hợp đồng làm việc cho một công ty \(Y\) với lương tháng đầu là \(6\) triệu. Trong điều khoản về lương, nếu anh \(X\) hoàn thành nhiệm vụ thì cứ sau \(6\) tháng được tăng \(15\% \) so với mức lương trước đó. Trong suốt quá trình làm việc, anh \(X\) đều hoàn thành nhiệm vụ của mình và được tăng lương đúng kỳ hạn.
a) Mức lương của anh \(X\) ở tháng thứ \(11\) kể từ khi ký hợp đồng lao động là \(6,9\) triệu đồng.
b) Coi mỗi \(6\) tháng anh \(X\) nhận lương như nhau là một kỳ và \({u_n}\) là lương mỗi tháng của kỳ thứ \(n\), khi đó \(\left( {{u_n}} \right)\) là một cấp số cộng với công sai \(d = 1,15\).
c) Tổng số tiền anh \(X\) nhận được từ tiền lương của công ty \(Y\) sau \(4\) năm kể từ ngày ký hợp đồng (làm tròn đến hàng phần trăm) là \(494,17\) triệu đồng.
d) Khi nhận lương hàng tháng, nếu anh \(X\) phải đóng bảo hiểm thất nghiệp \(1,5\% \) số tiền lương được nhận thì sau \(10\) năm kể từ ngày ký hợp đồng anh \(X\) đã đóng số tiền bảo hiểm thất nghiệp (làm tròn đến hàng phần trăm) là \(55,32\) triệu đồng.
Anh \(X\) nhận hợp đồng làm việc cho một công ty \(Y\) với lương tháng đầu là \(6\) triệu. Trong điều khoản về lương, nếu anh \(X\) hoàn thành nhiệm vụ thì cứ sau \(6\) tháng được tăng \(15\% \) so với mức lương trước đó. Trong suốt quá trình làm việc, anh \(X\) đều hoàn thành nhiệm vụ của mình và được tăng lương đúng kỳ hạn.
a) Mức lương của anh \(X\) ở tháng thứ \(11\) kể từ khi ký hợp đồng lao động là \(6,9\) triệu đồng.
b) Coi mỗi \(6\) tháng anh \(X\) nhận lương như nhau là một kỳ và \({u_n}\) là lương mỗi tháng của kỳ thứ \(n\), khi đó \(\left( {{u_n}} \right)\) là một cấp số cộng với công sai \(d = 1,15\).
c) Tổng số tiền anh \(X\) nhận được từ tiền lương của công ty \(Y\) sau \(4\) năm kể từ ngày ký hợp đồng (làm tròn đến hàng phần trăm) là \(494,17\) triệu đồng.
d) Khi nhận lương hàng tháng, nếu anh \(X\) phải đóng bảo hiểm thất nghiệp \(1,5\% \) số tiền lương được nhận thì sau \(10\) năm kể từ ngày ký hợp đồng anh \(X\) đã đóng số tiền bảo hiểm thất nghiệp (làm tròn đến hàng phần trăm) là \(55,32\) triệu đồng.Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 12 có đáp án !!
Quảng cáo
Trả lời:
a) Đúng. Gọi mức lương mỗi tháng của anh \(X\) trong \(6\) tháng đầu là \({u_1} = 6\) triệu đồng thì mức lương anh \(X\) ở tháng thứ \(11\) là \({u_2} = {u_1} + {u_1} \cdot 15\% = {u_1}\left( {1 + 15\% } \right) = 6 \cdot \left( {1 + \frac{{15}}{{100}}} \right) = 6,9\) triệu đồng.
b) Sai. Gọi mức lương mỗi tháng của anh \(X\) trong \(6\) tháng đầu là \({u_1} = 6\) triệu đồng thì mức lương anh \(X\) ở mỗi tháng kỳ \(2\) là \({u_2} = {u_1} + {u_1} \cdot 15\% = {u_1}\left( {1 + 15\% } \right)\).
Mức lương mỗi tháng của kỳ thứ \(3\) là \({u_3} = {u_2} + {u_2} \cdot 15\% = {u_2}\left( {1 + 15\% } \right) = {u_1}{\left( {1 + 15\% } \right)^2}\).
….
Mức lương mỗi tháng của kỳ thứ \(n\) là \({u_n} = {u_1}{\left( {1,15} \right)^{n - 1}}\)
Vậy \(\left( {{u_n}} \right)\) là cấp số nhân với công bội là \(q = 1,15\).
c) Đúng. Ta có lương mỗi tháng của anh \(X\) theo từng kỳ \(6\) tháng là một cấp số nhân có \({u_1} = 6\), công bội \(q = 1,15\), khi đó tổng số tiền lương nhận được sau \(4\) năm (\(8\) kỳ) là
\({S_8} = 6\left( {{u_1} + {u_2} + ... + {u_8}} \right)\) \( = 6 \cdot 6 \cdot \frac{{1 - 1,{{15}^8}}}{{1 - 1,15}} \approx 494,17\) triệu đồng.
d) Đúng. Ta có số tiền bảo hiểm thất nghiệp anh \(X\) phải đóng trong \(10\) năm (\(20\) kỳ) là
\({T_{20}} = 6 \cdot 1,5\% \left( {{u_1} + {u_2} + ... + {u_{20}}} \right)\)\( = 6 \cdot 1,5\% \cdot {u_1}\frac{{1 - 1,{{15}^{20}}}}{{1 - 1,15}} \approx 55,32\) triệu đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
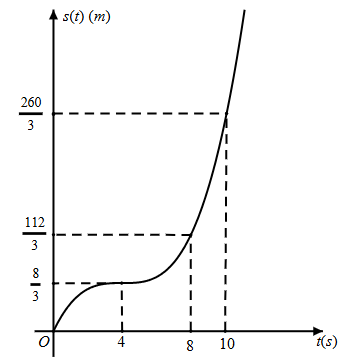
Giả sử \(s\left( t \right) = a{t^3} + b{t^2} + ct + d\,\,\left( {a \ne 0} \right).\)
Vì đồ thị hàm số \(s\left( t \right)\) đi qua các điểm \(\left( {0\,;\,0} \right)\), \(\left( {4\,;\,\frac{8}{3}\,} \right)\), \(\left( {8\,;\,\,\frac{{112}}{3}} \right)\) và \(\left( {10\,;\frac{{260}}{3}} \right)\) nên ta có
\(\left\{ \begin{array}{l}d = 0\\64a + 16b + 4c = \frac{8}{3}\\512a + 64b + 8c = \frac{{112}}{3}\\1000a + 100b + 10c = \frac{{260}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{6}\\b = - 1\\c = 2\\d = 0\end{array} \right.\). Do đó \(s\left( t \right) = \frac{1}{6}{t^3} - {t^2} + 2t.\)
Ta có \(v\left( t \right) = s'\left( t \right) = \frac{1}{2}{t^2} - 2t + 2 \Rightarrow \)\(v'\left( t \right) = t - 2 = 0 \Leftrightarrow t = 2.\)
Bảng biến thiên:
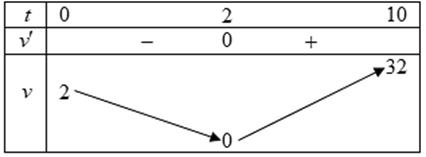
Dựa vào bảng biến thiên, từ giây thứ \(2\) trở đi vận tốc của vật tăng dần theo thời gian. Do đó trong \(10\) giây đầu tiên, khoảng thời gian vật chuyển động nhanh dần kéo dài trong \(8\) giây.
Đáp án: \(8\).
Lời giải
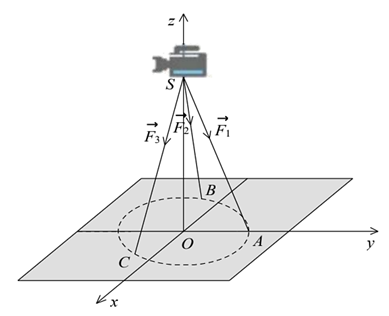
\(\overrightarrow {SA} = \left( {0;1; - 5} \right),\,\,\,\overrightarrow {SB} = \left( { - \frac{{\sqrt 3 }}{2}; - \frac{1}{2}; - 5} \right),\,\,\overrightarrow {SC} \left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2}; - 5} \right)\,\).
\(\overrightarrow {AB} = \left( { - \frac{{\sqrt 3 }}{2}; - \frac{3}{2};0} \right),\,\,\,\overrightarrow {BC} = \left( {\sqrt 3 ;0;0} \right),\,\,\overrightarrow {AC} = \left( {\frac{{\sqrt 3 }}{2}; - \frac{3}{2};0} \right) \Rightarrow AB = BC = AC = 3\).
Ta có \(SA = SB = SC = \sqrt {26} \) nên hình chiếu của \(S\) trên \(\left( {ABC} \right)\) là tâm đường tròn ngoại tiếp \(\Delta ABC\) mà lại có \(\Delta ABC\) đều nên \(SO \bot \left( {ABC} \right)\).
Giả sử \(\overrightarrow {{F_1}} = k\overrightarrow {SA} ,\,\,\,\overrightarrow {{F_2}} = k\overrightarrow {SB} ,\,\,\,\overrightarrow {{F_3}} = k\overrightarrow {SC} \,\,\,\left( {k > 0} \right)\)
\( \Rightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = k\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right) = \left( {0;0; - 15k} \right)\).
Theo bài ta lại có \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right| = 60 \Rightarrow 15k = 60 \Rightarrow k = 4\).
Vậy \(\left| {\overrightarrow {{F_1}} } \right| + \left| {\overrightarrow {{F_2}} } \right| + \left| {\overrightarrow {{F_3}} } \right| = 4\left( {SA + SB + SC} \right) = 12\sqrt {26} \) (N).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.