Quảng cáo
Trả lời:
Giải bởi Vietjack
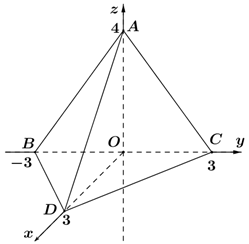
b) Một vectơ pháp tuyến của mặt phẳng \(\left( {ABD} \right)\) là \({\vec n_1} = \left( {4;\, - 4;\,3} \right)\)
Một vectơ pháp tuyến của mặt phẳng \(\left( {Oyz} \right)\) là \(\overrightarrow i = \left( {1;\,0;\,0} \right)\)
Khi đóChọn Sai
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
Nhắn tin Zalo
Hỏi bài tập