PHẦN III. (1,5 điểm) Câu trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
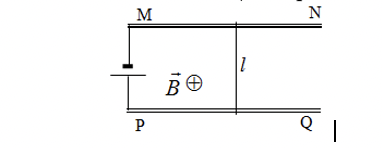
Thanh \[L\] có chiều dài \(10\,\,cm\) nặng \(40\,\,gam,\) điện trở \(1,9\,\,\Omega ,\) tựa trên hai thanh \[MN\] và \[PQ\] có điện trở không đáng kể. Suất điện động của nguồn \(4\,\,V,\) điện trở trong \(0,1\,\,\Omega .\) Mạch điện đặt trong từ trường đều \[B = 0,1\,\,T,\] vuông góc với mặt phẳng khung. Thanh \[L\] chuyển động với gia tốc là bao nhiêu m/s2 ? ( Kết quả làm tròn đến chữ số hàng phần mười)
PHẦN III. (1,5 điểm) Câu trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Thanh \[L\] có chiều dài \(10\,\,cm\) nặng \(40\,\,gam,\) điện trở \(1,9\,\,\Omega ,\) tựa trên hai thanh \[MN\] và \[PQ\] có điện trở không đáng kể. Suất điện động của nguồn \(4\,\,V,\) điện trở trong \(0,1\,\,\Omega .\) Mạch điện đặt trong từ trường đều \[B = 0,1\,\,T,\] vuông góc với mặt phẳng khung. Thanh \[L\] chuyển động với gia tốc là bao nhiêu m/s2 ? ( Kết quả làm tròn đến chữ số hàng phần mười)

Quảng cáo
Trả lời:
ĐÁP ÁN : 0,5 m/s2
Ta có cường độ dòng điện qua thanh \(L\) là \(I = \frac{{\rm{E}}}{{R + r}} = \frac{4}{{1,9 + 0,1}} = 2\,\,A.\)
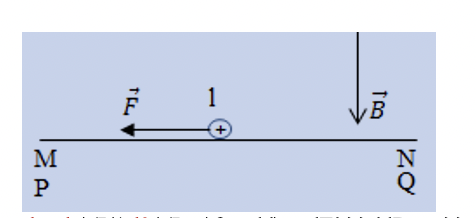
Lực từ tác dụng lên thanh được biểu diễn như hình vẽ trên. Thanh sẽ trượt trên \(MN\) và \(PQ\) với gia tốc \(a\)\( \Rightarrow \,F = ma.\)
Vậy \(F = BIL = ma \Rightarrow a = \frac{{BIL}}{m} = \frac{{0,1.2.0,1}}{{0,04}} = 0,{\rm{5}}\,\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi nhiệt dung mỗi quả cầu là Cq và nhiệt dung của nước là Cn
\[{C_q}(t - {t_1}) = {C_n}({t_1} - {t_0}) \Rightarrow {C_q}(100 - 40) = {C_n}(40 - 20) \Rightarrow {C_n} = 3{C_q}\]
Để nhiệt độ cân bằng là 90°C thì cần thả q quả cầu có:
\[q{C_q}(t - {t_2}) = {C_n}({t_2} - {t_0}) \Rightarrow q(100 - 90) = 3(90 - 20) \Rightarrow q = 21\]quả
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 6-5-4-3-2-1
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.