Một bình kín có thể tích không đổi chứa một lượng khí nhất định. Chất khí trong bình được làm lạnh. Điều gì xảy ra với áp suất chất khí và động năng trung bình của các phân tử khí trong bình?
Một bình kín có thể tích không đổi chứa một lượng khí nhất định. Chất khí trong bình được làm lạnh. Điều gì xảy ra với áp suất chất khí và động năng trung bình của các phân tử khí trong bình?
A. Áp suất chất khí giảm, động năng trung bình của các phân tử khí giảm.
B. Áp suất chất khí giảm, động năng trung bình của các phân tử khí tăng.
C. Áp suất chất khí tăng, động năng trung bình của các phân tử khí giảm.
Quảng cáo
Trả lời:
Phương pháp:
- Làm lạnh khí: Nhiệt độ giảm.
- Lý thuyết về động năng trung bình của các phân tử khí và áp suất chất khí.
Cách giải:
Áp suất chất khí: \(p = \mu kT\)
Động năng trung bình của các phân tử khí: \({W_d} = \frac{3}{2}kT\)
Ta thấy, khi làm lạnh nhiệt độ giảm dẫn đến áp suất và động năng trung bình của các phân tử khí giảm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
Mối quan hệ của hai nhiệt độ: \(\frac{{{\rm{t'}} + 2}}{{102 + 2}} = \frac{{{\rm{t}}\left( {{\;^o}{\rm{C}}} \right)}}{{100}}\)
Cách giải:
Nếu nhiệt độ đo bởi nhiệt kế này là: \({\rm{t'}} = {50^ \circ }{\rm{C}}\) thì nhiệt độ theo thang đo nhiệt độ Celsius là:
\(\frac{{{\rm{t'}} + 2}}{{102 + 2}} = \frac{{{\rm{t}}\left( {{\;^{\rm{o}}}{\rm{C}}} \right)}}{{100}} \Rightarrow \frac{{50 + 2}}{{102 + 2}} = \frac{{{\rm{t}}\left( {{\;^{\rm{o}}}{\rm{C}}} \right)}}{{100}} \Rightarrow {\rm{t}}\left( {{\;^{\rm{o}}}{\rm{C}}} \right) = 50\)
Đáp án: 50.
Câu 2
Lời giải
Phương pháp:
Tính độ chia của nhiệt kế suy ra nhiệt độ hiển thị bằng cách nhân độ chia với vị trí hiện tại.
Cách giải:
Điểm đóng băng của nước \({0^ \circ }{\rm{C}} \to \) ứng với vạch số 1 cm.
Điểm sôi của nước \({100^ \circ }{\rm{C}} \to \) ứng với vạch số 11 cm.
Do đó mỗi 1 cm vạch chia trên thước ứng với \({10^ \circ }{\rm{C}}\)
Nhiệt độ đang hiển thị trên nhiệt kế ứng với \(6,6{\rm{\;cm}}\) từ điểm đóng băng
\( \to \) Nhiệt độ đang hiển thị là \({66^ \circ }{\rm{C}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
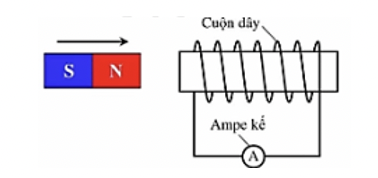
A. Tăng số vòng của cuộn dây.
B. Tăng điện trở của ampe kế.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.