Một loại linh kiện do hai nhà máy số I , số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy \({\rm{I}},{\rm{II}}\) lần lượt là: \(4\% ;3\% \). Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó.
a) Tính xác suất để linh kiện được lấy ra là linh kiện tốt.
b) Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao nhất?
Một loại linh kiện do hai nhà máy số I , số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy \({\rm{I}},{\rm{II}}\) lần lượt là: \(4\% ;3\% \). Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó.
a) Tính xác suất để linh kiện được lấy ra là linh kiện tốt.
b) Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao nhất?
Quảng cáo
Trả lời:
a) Xét hai biến cố:
A: "Linh kiện được lấy ra từ lô hàng là linh kiện tốt”;
B: "Linh kiện được lấy ra từ lô hàng do nhà máy I sản xuất".
Vi lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II nên \(P(B) = \frac{{80}}{{80 + 120}} = 0,4\), suy ra \(P(\bar B) = 1 - 0,4 = 0,6\).
Vì tỉ lệ phế phẩm của các nhà máy I, II lần lượt là: \(4\% ;3\% \) nên tỉ lệ thành phẩm (linh kiện tốt) của các nhà máy I, II lần lượt là \(96\% ;97\% \).
Do đó \({\rm{P}}({\rm{A}}\mid {\rm{B}}) = 0,96\) và \({\rm{P}}({\rm{A}}\mid \bar B) = 0,97\).
Áp dụng công thức xác suất toàn phần, ta có xác suất để linh kiện được lấy ra là linh kiện tốt là:
\({\rm{P}}({\rm{A}}) = {\rm{P}}({\rm{B}}) \cdot {\rm{P}}({\rm{A}}\mid {\rm{B}}) + {\rm{P}}(\bar B) \cdot {\rm{P}}({\rm{A}}\mid \bar B) = 0,4 \cdot 0,96 + 0,6 \cdot 0,97 = 0,966.\)
b) Xét biến cố C: "Linh kiện được lấy ra từ lô hàng là linh kiện phế phẩm".
Khi đó, ta có \({\rm{C}} = \bar A\). Suy ra \({\rm{P}}({\rm{C}}) = {\rm{P}}(\bar A) = 1 - {\rm{P}}({\rm{A}}) = 1 - 0,966 = 0,034\).
Theo bài ra ta có: \(P(C\mid B) = 4\% = 0,04\).
Do đó, nếu linh kiện được lấy ra là linh kiện phế phẩm thì xác suất sản phẩm đó do nhà máy I sản xuất là: \({\rm{P}}({\rm{B}}\mid {\rm{C}}) = \frac{{P(B) \cdot P(C\mid B)}}{{P(C)}} = \frac{{0,4 \cdot 0,04}}{{0,034}} = \frac{8}{{17}}\).
Nếu linh kiện được lấy ra là linh kiện phế phẩm thì xác suất sản phẩm đó do nhà máy II sản xuất là: \({\rm{P}}(\bar B\mid {\rm{C}}) = 1 - {\rm{P}}({\rm{B}}\mid {\rm{C}}) = 1 - \frac{8}{{17}} = \frac{9}{{17}}\).
Vi \(\frac{9}{{17}} > \frac{8}{{17}}\) nên nếu linh kiện được lấy ra là linh kiện phế phẩm thì xác suất linh kiện đó do nhà máy II sản xuất là cao hơn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Xét hai biến cố: \(K\) : "Người được chọn ra không mắc bệnh";
\(D\) : "Người được chọn ra có phản ứng dương tính".
Do tỉ lệ người mắc bệnh là \(0,1\% = 0,001\) nên \({\rm{P}}(K) = 1 - 0,001 = 0,999\).
Trong số những người không mắc bệnh có \(5\% \) số người có phản ứng dương tính nên \({\rm{P}}(D\mid K) = 5\% = 0,05\). Vì ai mắc bệnh khi xét nghiệm cũng có phản ứng dương tính nên \({\rm{P}}(D\mid \bar K) = 1\).
Sơ đồ hình cây ở Hình 3 biểu thi tình huống đã cho.
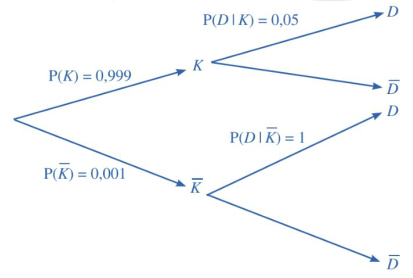
b) Ta thấy: Khả năng mắc bệnh của một người xét nghiệm có phản ứng dương tính chính là \({\rm{P}}(\bar K\mid D)\). Áp dụng công thức Bayes, ta có:
\({\rm{P}}(\bar K\mid D) = \frac{{{\rm{P}}(\bar K) \cdot {\rm{P}}(D\mid \bar K)}}{{{\rm{P}}(\bar K) \cdot {\rm{P}}(D\mid \bar K) + {\rm{P}}(K) \cdot {\rm{P}}(D\mid K)}} = \frac{{0,001}}{{0,001 + 0,999 \cdot 0,05}} \approx 1,96\% .\)
Vậy xác suất mắc bệnh của một người xét nghiệm có phản ứng dương tính là \(1,96\% \).
Lời giải
Gọi \(A\) là biến cố: "Bà \(N\) bị bệnh hiểm nghèo \(Y\) "; \(B\) là biến cố: "Xét nghiệm cho kết quả dương tính".
a) Trước khi tiến hành xét nghiệm, xác suất không mắc bệnh hiểm nghèo Y của bà N là
\(P(\bar A) = 1 - P(A) = 1 - 0,005 = 0,995.{\rm{ }}\)
b) Ta cần tính \(P(\bar A\mid \bar B)\).
Theo công thức Bayes ta có: \(P(\bar A\mid \bar B) = \frac{{P(\bar A) \cdot P(\bar B\mid \bar A)}}{{P(\bar A) \cdot P(\bar B\mid \bar A) + P(A) \cdot P(\bar B\mid A)}}.\)
\(P(\bar B\mid \bar A)\) là xác suất để bà \(N\) có xét nghiệm là âm tính nếu bà \(N\) không bị bệnh \(Y\).
Theo bài ra ta có: \(P(\bar B\mid \bar A) = 0,97{\rm{;}}\)
\(P(\bar B\mid A)\) là xác suất để bà N có xét nghiệm âm tính nếu bà N bị bệnh Y
\(P(\bar B\mid A) = 1 - 0,94 = 0,06.{\rm{ }}\)
Thay vào công thức Bayes ta có: \(P(\bar A\mid \bar B) = \frac{{0,995 \cdot 0,97}}{{0,995 \cdot 0,97 + 0,005 \cdot 0,06}} \approx 0,9997.\)
Như vậy, với xét nghiệm cho kết quả âm tính, xác suất không mắc bệnh Y của bà N tăng lên thành \(99,97\% \) (trước xét nghiệm là \(99,5\% \) ).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.