Người ta cung cấp một nhiệt lượng \(1,5{\rm{\;J}}\) cho chất khí đựng trong một xilanh đặt nằm ngang. Khi nở ra đẩy pittông di chuyển đều một đoạn 5 cm . Biết lực ma sát giữa pittông và xilanh có độ lớn 20 N.
Người ta cung cấp một nhiệt lượng \(1,5{\rm{\;J}}\) cho chất khí đựng trong một xilanh đặt nằm ngang. Khi nở ra đẩy pittông di chuyển đều một đoạn 5 cm . Biết lực ma sát giữa pittông và xilanh có độ lớn 20 N.
A. \( - 1,5{\rm{\;J}}\).
Quảng cáo
Trả lời:
Phương pháp:
Áp dụng công thức \(A = F.s\) và \({\rm{\Delta }}U = A + Q\)
Cách giải:
Vì khí nở ra đẩy pittong chuyển động đều nên \(F = {F_m}\)
Công do chất khí tạo ra để thắng lực ma sát có độ lớn là:
\(\left| A \right| = F.s = 20.0,05 = 1J\)
Chất khí nhận nhiệt và thực hiện công nên \(\left\{ {\begin{array}{*{20}{l}}{Q > 0}\\{A < 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{Q = 1,5{\rm{\;J}}}\\{A = - 1{\rm{\;J}}}\end{array}} \right.} \right.\)
Độ biến thiên nội năng là: \({\rm{\Delta }}U = A + Q = - 1 + 1,5 = 0,5J\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
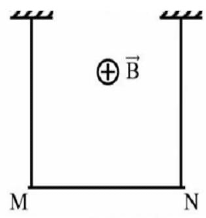
- Điều kiện cân bằng của dây.
- Lực từ tác dụng lên dây có độ lớn: \(F = BI\ell \)
Cách giải:
Lực căng dây bằng không khi đó lực từ cân bằng với trọng lực:
\(F = P \Rightarrow BI\ell = mg\)
\( \Rightarrow I = \frac{{mg}}{{B\ell }} = \frac{{0,05.10}}{{0,04}} = 12,5\left( {\rm{A}} \right)\)
Câu 2
Lời giải
Phương pháp:
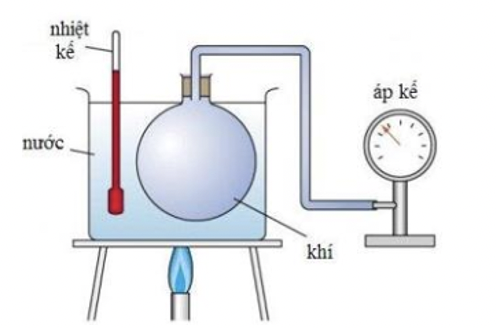
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
Cách giải:
Trạng thái \(1:\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1}}\\{{T_1} = {{627}^ \circ }{\rm{C}} + 273 = 900{\rm{\;K}}}\end{array}} \right.\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 1,2{p_1}}\\{{V_2} = \frac{{{V_1}}}{3}}\\{{T_2} = {\rm{?\;}}}\end{array}} \right.\)
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
\( \Rightarrow \frac{{{p_1}{V_1}}}{{900}} = \frac{{1,2{p_1}.\frac{{{V_1}}}{3}}}{{{T_2}}} \Rightarrow {T_2} = 360{\rm{\;K}}\)
Với \({T_2} = 360{\rm{\;K}} \Rightarrow {t_2} = {87^ \circ }{\rm{C}}\)
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.