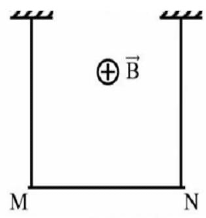
Một khung dây dẫn kín, phẳng có diện tích \(10{\rm{\;c}}{{\rm{m}}^2}\), gồm 100 vòng dây, đặt trong từ trường có vectơ cảm ứng từ vuông góc với mặt phẳng khung dây. Độ lớn cảm ứng từ biến thiên theo thời gian như đồ thị Hình vẽ. Độ lớn suất điện động xuất hiện trong khung dây trong khoảng thời gian 0 đến \(0,1{\rm{\;s}}\).
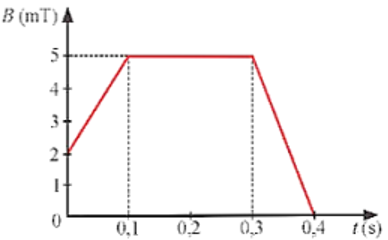
Một khung dây dẫn kín, phẳng có diện tích \(10{\rm{\;c}}{{\rm{m}}^2}\), gồm 100 vòng dây, đặt trong từ trường có vectơ cảm ứng từ vuông góc với mặt phẳng khung dây. Độ lớn cảm ứng từ biến thiên theo thời gian như đồ thị Hình vẽ. Độ lớn suất điện động xuất hiện trong khung dây trong khoảng thời gian 0 đến \(0,1{\rm{\;s}}\).

A. \({3.10^{ - 3}}{\rm{\;V}}\)
Quảng cáo
Trả lời:
Phương pháp:
Áp dụng công thức \(\left| {{e_c}} \right| = \left| {\frac{{{\rm{\Delta }}\phi }}{{{\rm{\Delta }}t}}} \right|\)
Cách giải:
Độ lớn suất điện động xuất hiện trong khung dây trong khoảng thời gian 0 đến \(0,1{\rm{\;s}}\) là:
\(\left| {{e_c}} \right| = \left| {\frac{{{\rm{\Delta }}\phi }}{{{\rm{\Delta }}t}}} \right| = \left| {\frac{{{\phi _{0,1}} - {\phi _0}}}{{0,1 - 0}}} \right| = \left| {\frac{{NS{\rm{cos}}\alpha \left( {{B_{0,1}} - {B_0}} \right)}}{{0,1 - 0}}} \right|\)
\( \Rightarrow \left| {{e_c}} \right| = \left| {\frac{{{{100.10.10}^{ - 4}}.\cos {0^o}.\left( {5 - 2} \right){{.10}^{ - 3}}}}{{0,1}}} \right| = {3.10^{ - 3}}\left( V \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
- Điều kiện cân bằng của dây.
- Lực từ tác dụng lên dây có độ lớn: \(F = BI\ell \)
Cách giải:
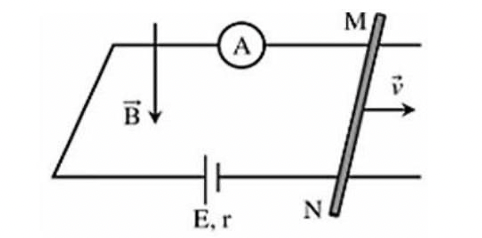
Lực căng dây bằng không khi đó lực từ cân bằng với trọng lực:
\(F = P \Rightarrow BI\ell = mg\)
\( \Rightarrow I = \frac{{mg}}{{B\ell }} = \frac{{0,05.10}}{{0,04}} = 12,5\left( {\rm{A}} \right)\)
Câu 2
Lời giải
Phương pháp:
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
Cách giải:
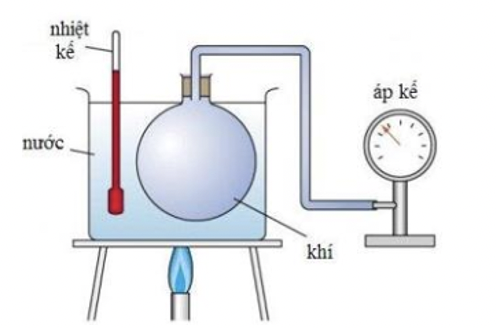
Trạng thái \(1:\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1}}\\{{T_1} = {{627}^ \circ }{\rm{C}} + 273 = 900{\rm{\;K}}}\end{array}} \right.\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 1,2{p_1}}\\{{V_2} = \frac{{{V_1}}}{3}}\\{{T_2} = {\rm{?\;}}}\end{array}} \right.\)
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
\( \Rightarrow \frac{{{p_1}{V_1}}}{{900}} = \frac{{1,2{p_1}.\frac{{{V_1}}}{3}}}{{{T_2}}} \Rightarrow {T_2} = 360{\rm{\;K}}\)
Với \({T_2} = 360{\rm{\;K}} \Rightarrow {t_2} = {87^ \circ }{\rm{C}}\)
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.