PHẦN II: CÂU TRẮC NGHIỆM ĐÚNG SAI
Một bát bằng đồng nặng 150 g đựng 220 g nước đều ở nhiệt độ \({20^ \circ }{\rm{C}}\). Một miếng đồng hình trụ khối lượng 300 g ở nhiệt độ cao rơi vào bát nước làm nước sôi và chuyển \(5,00{\rm{\;g}}\) nước thành hơi. Nhiệt độ cuối của hệ là \({100^ \circ }{\rm{C}}\). Biết nhiệt dung riêng của đồng là \(380{\rm{\;J/kg}}.{\rm{K}}\); nhiệt dung riêng của nước \({c_{{{\rm{H}}_2}{\rm{O}}}} = 4200{\rm{\;J}}/{\rm{kg}}.{\rm{K}}\) và nhiệt hoá hơi riêng của nước \(L = {2,26.10^6}{\rm{\;J}}/{\rm{kg}}.{\rm{K}}\). Bỏ qua sự trao đổi nhiệt với không khí. Trong các câu sau đây, câu nào đúng, sai?
a) Nhiệt lượng bát đồng nhận được để tăng nhiệt độ từ \({20^ \circ }{\rm{C}}\) đến \({100^ \circ }{\rm{C}}\) là 4560 J .
b) Bát đồng và nước nhận nhiệt lượng từ miếng đồng.
c) Nhiệt lượng mà nước nhận được để tăng nhiệt độ từ \({20^ \circ }{\rm{C}}\) đến \({100^ \circ }{\rm{C}}\) là 124320 J .
d) Nhiệt độ ban đầu của miếng đồng gần đúng là \({887,5^ \circ }{\rm{C}}\).
PHẦN II: CÂU TRẮC NGHIỆM ĐÚNG SAI
Một bát bằng đồng nặng 150 g đựng 220 g nước đều ở nhiệt độ \({20^ \circ }{\rm{C}}\). Một miếng đồng hình trụ khối lượng 300 g ở nhiệt độ cao rơi vào bát nước làm nước sôi và chuyển \(5,00{\rm{\;g}}\) nước thành hơi. Nhiệt độ cuối của hệ là \({100^ \circ }{\rm{C}}\). Biết nhiệt dung riêng của đồng là \(380{\rm{\;J/kg}}.{\rm{K}}\); nhiệt dung riêng của nước \({c_{{{\rm{H}}_2}{\rm{O}}}} = 4200{\rm{\;J}}/{\rm{kg}}.{\rm{K}}\) và nhiệt hoá hơi riêng của nước \(L = {2,26.10^6}{\rm{\;J}}/{\rm{kg}}.{\rm{K}}\). Bỏ qua sự trao đổi nhiệt với không khí. Trong các câu sau đây, câu nào đúng, sai?
a) Nhiệt lượng bát đồng nhận được để tăng nhiệt độ từ \({20^ \circ }{\rm{C}}\) đến \({100^ \circ }{\rm{C}}\) là 4560 J .
b) Bát đồng và nước nhận nhiệt lượng từ miếng đồng.
c) Nhiệt lượng mà nước nhận được để tăng nhiệt độ từ \({20^ \circ }{\rm{C}}\) đến \({100^ \circ }{\rm{C}}\) là 124320 J .
d) Nhiệt độ ban đầu của miếng đồng gần đúng là \({887,5^ \circ }{\rm{C}}\).
Quảng cáo
Trả lời:
Phương pháp:
- Nhiệt lượng cần cung cấp cho một chất để làm tăng nhiệt độ: \(Q = mc{\rm{\Delta }}t\).
- Nhiệt lượng cung cấp cho quá trình hóa hơi: \(Q = mL\).
- Áp dụng phương trình cân bằng nhiệt.
Cách giải:
a) Nhiệt lượng mà bát đồng nhận được để tăng nhiệt độ từ \({20^ \circ }{\rm{C}}\) đến \({100^ \circ }{\rm{C}}\) là:
\(Q = {m_b}{c_{Cu}}{\rm{\Delta }}t = 0,15.380.\left( {100 - 20} \right) = 4560\left( J \right)\)
\( \to \) a đúng.
b) Bát đồng và nước tăng nhiệt độ nên nhận nhiệt lượng từ miếng đồng.
\( \to \) b đúng.
c) Nhiệt lượng mà nước nhận được để tăng nhiệt độ từ \({20^ \circ }{\rm{C}}\) đến \({100^ \circ }{\rm{C}}\):
\(Q' = {m_n}{c_{{H_2}O}}{\rm{\Delta }}t = 0,22.4200.\left( {100 - 20} \right) = 73920\left( J \right)\)
\( \to \) c sai.
d) Áp dụng phương trình cân bằng nhiệt:
\({Q_{thu}} = {Q_{toa}} \Rightarrow \left( {{m_b}{c_{Cu}} + {m_n}{c_{{H_2}{\rm{O}}}}} \right){\rm{\Delta }}t + {m_h}L = {m_m}{c_{Cu}}\left( {t - 100} \right)\)
Thay số vào ta được:
\(\left( {0,15.380 + 0,22.4200} \right)\left( {100 - 20} \right) + {5.10^{ - 3}}{.2,26.10^{ - 6}} = 0,3.380.\left( {t - 100} \right)\)
\( \Rightarrow t \approx {788,42^ \circ }C\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
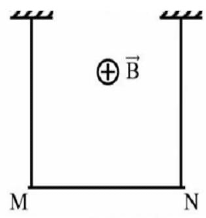
- Điều kiện cân bằng của dây.
- Lực từ tác dụng lên dây có độ lớn: \(F = BI\ell \)
Cách giải:
Lực căng dây bằng không khi đó lực từ cân bằng với trọng lực:
\(F = P \Rightarrow BI\ell = mg\)
\( \Rightarrow I = \frac{{mg}}{{B\ell }} = \frac{{0,05.10}}{{0,04}} = 12,5\left( {\rm{A}} \right)\)
Câu 2
Lời giải
Phương pháp:
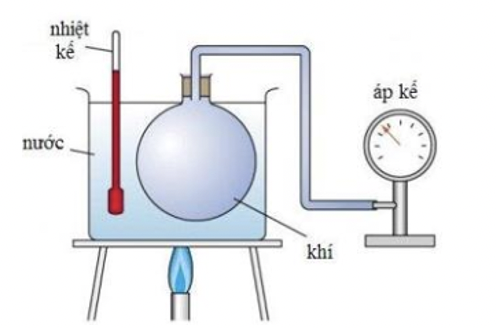
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
Cách giải:
Trạng thái \(1:\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1}}\\{{T_1} = {{627}^ \circ }{\rm{C}} + 273 = 900{\rm{\;K}}}\end{array}} \right.\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 1,2{p_1}}\\{{V_2} = \frac{{{V_1}}}{3}}\\{{T_2} = {\rm{?\;}}}\end{array}} \right.\)
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
\( \Rightarrow \frac{{{p_1}{V_1}}}{{900}} = \frac{{1,2{p_1}.\frac{{{V_1}}}{3}}}{{{T_2}}} \Rightarrow {T_2} = 360{\rm{\;K}}\)
Với \({T_2} = 360{\rm{\;K}} \Rightarrow {t_2} = {87^ \circ }{\rm{C}}\)
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.