Đổ 2 lít nước ở \({25^ \circ }{\rm{C}}\) vào một ấm nhôm có khối lượng 800 gam và sau đó đun bằng bếp điện. Sau 40 phút thì đã có \(20{\rm{\% }}\) khối lượng nước đã hóa hơi ở nhiệt độ sôi \({100^ \circ }{\rm{C}}\). Biết rằng \(80{\rm{\% }}\) nhiệt lượng mà bếp cung cấp được dùng vào việc đun nước. Cho biết nhiệt dung riêng của nước là \(4190{\rm{\;J}}/{\rm{kg}}.{\rm{K}}\), của nhôm là \(880{\rm{\;J/kg}}{\rm{.K}}\), nhiệt hóa hơi của nước ở \({100^ \circ }{\rm{C}}\) là \({2,26.10^6}{\rm{\;J/kg}}\), khối lượng riêng của nước là 1kg/ lít. Công suất cung cấp nhiệt của bếp điện là bao nhiêu W? (Kết quả làm tròn đến 0 chữ số sau dấu phẩy thập phân).
Đổ 2 lít nước ở \({25^ \circ }{\rm{C}}\) vào một ấm nhôm có khối lượng 800 gam và sau đó đun bằng bếp điện. Sau 40 phút thì đã có \(20{\rm{\% }}\) khối lượng nước đã hóa hơi ở nhiệt độ sôi \({100^ \circ }{\rm{C}}\). Biết rằng \(80{\rm{\% }}\) nhiệt lượng mà bếp cung cấp được dùng vào việc đun nước. Cho biết nhiệt dung riêng của nước là \(4190{\rm{\;J}}/{\rm{kg}}.{\rm{K}}\), của nhôm là \(880{\rm{\;J/kg}}{\rm{.K}}\), nhiệt hóa hơi của nước ở \({100^ \circ }{\rm{C}}\) là \({2,26.10^6}{\rm{\;J/kg}}\), khối lượng riêng của nước là 1kg/ lít. Công suất cung cấp nhiệt của bếp điện là bao nhiêu W? (Kết quả làm tròn đến 0 chữ số sau dấu phẩy thập phân).
Quảng cáo
Trả lời:
Phương pháp:
+ Sử dụng công thức: \({\rm{m}} = {\rm{DV}}\)
+ Áp dụng phương trình cân bằng nhiệt.
Cách giải:
Khối lượng của nước trong ấm: \(m = DV = 1.2 = 2\left( {{\rm{kg}}} \right)\)
Nhiệt lượng mà ấm đã cung cấp để đun nước là: \(Q = P.t\)
Nhiệt lượng mà ấm đã thu vào để sôi và hóa hơi một phần là:
\(Q' = \left( {{m_n}{c_n} + {m_{Al}}{c_{Al}}} \right){\rm{\Delta }}t + 20{\rm{\% }}{m_n}L\)
\( \Rightarrow Q' = \left( {2.4190 + 0,8.880} \right)\left( {100 - 25} \right) + 20{\rm{\% }}{.2.2,26.10^6}\)
\( \Rightarrow Q' = 1585300\left( {\rm{J}} \right)\)
Vì chỉ cố \(80{\rm{\% }}\) nhiệt lượng mà bếp cung cấp được dùng vào việc đun nước nên ta có:
\(80{\rm{\% }}Q = Q' \Rightarrow 80{\rm{\% }}.P.40.60 = 1585300\)
\( \Rightarrow P \approx 826\) (W)
Đáp án: 826.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
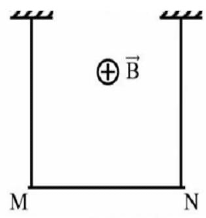
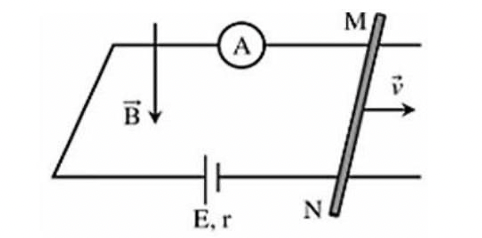
- Điều kiện cân bằng của dây.
- Lực từ tác dụng lên dây có độ lớn: \(F = BI\ell \)
Cách giải:
Lực căng dây bằng không khi đó lực từ cân bằng với trọng lực:
\(F = P \Rightarrow BI\ell = mg\)
\( \Rightarrow I = \frac{{mg}}{{B\ell }} = \frac{{0,05.10}}{{0,04}} = 12,5\left( {\rm{A}} \right)\)
Câu 2
Lời giải
Phương pháp:
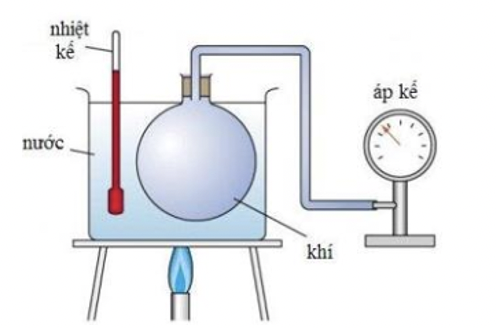
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
Cách giải:
Trạng thái \(1:\left\{ {\begin{array}{*{20}{l}}{{p_1}}\\{{V_1}}\\{{T_1} = {{627}^ \circ }{\rm{C}} + 273 = 900{\rm{\;K}}}\end{array}} \right.\)
Trạng thái 2: \(\left\{ {\begin{array}{*{20}{l}}{{p_2} = 1,2{p_1}}\\{{V_2} = \frac{{{V_1}}}{3}}\\{{T_2} = {\rm{?\;}}}\end{array}} \right.\)
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
\( \Rightarrow \frac{{{p_1}{V_1}}}{{900}} = \frac{{1,2{p_1}.\frac{{{V_1}}}{3}}}{{{T_2}}} \Rightarrow {T_2} = 360{\rm{\;K}}\)
Với \({T_2} = 360{\rm{\;K}} \Rightarrow {t_2} = {87^ \circ }{\rm{C}}\)
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.