Một vật có khối lượng \({{\rm{m}}_0}\left( {{\rm{kg}}} \right)\) được làm từ vật liệu có nhiệt dung riêng c phụ thuộc vào nhiệt độ t theo quy luật \(c\left( t \right) = {c_0}\left( {1 + \alpha {\rm{t}}} \right)\), trong đó \({c_0} = {1,3.10^3}\left( {{\rm{J/kg}}.{\rm{K}}} \right)\) và \(\alpha = {0,012^o}{C^{ - 1}}\). Đưa vật vào nhiệt lượng kế chứa \(0,5{\rm{\;}}{{\rm{m}}_0}\left( {{\rm{kg}}} \right)\) nước ở nhiệt độ \({{\rm{t}}_{01}} = {45^ \circ }{\rm{C}}\).Biết nhiệt độ ban đầu của vật là \({{\rm{t}}_0} = {0^ \circ }{\rm{C}}\), nhiệt dung riêng của nước là \({c_1} = 4200\left( {{\rm{J/kg}}.{\rm{K}}} \right)\). Bỏ qua nhiệt dung của nhiệt lượng kế và tổn thất nhiệt. Tìm nhiệt độ ổn định của nước trong nhiệt lượng kế? Kết quả tính bằng\({\;^ \circ }{\rm{C}}\) và làm tròn đến một chữ số thập phân.
Một vật có khối lượng \({{\rm{m}}_0}\left( {{\rm{kg}}} \right)\) được làm từ vật liệu có nhiệt dung riêng c phụ thuộc vào nhiệt độ t theo quy luật \(c\left( t \right) = {c_0}\left( {1 + \alpha {\rm{t}}} \right)\), trong đó \({c_0} = {1,3.10^3}\left( {{\rm{J/kg}}.{\rm{K}}} \right)\) và \(\alpha = {0,012^o}{C^{ - 1}}\). Đưa vật vào nhiệt lượng kế chứa \(0,5{\rm{\;}}{{\rm{m}}_0}\left( {{\rm{kg}}} \right)\) nước ở nhiệt độ \({{\rm{t}}_{01}} = {45^ \circ }{\rm{C}}\).Biết nhiệt độ ban đầu của vật là \({{\rm{t}}_0} = {0^ \circ }{\rm{C}}\), nhiệt dung riêng của nước là \({c_1} = 4200\left( {{\rm{J/kg}}.{\rm{K}}} \right)\). Bỏ qua nhiệt dung của nhiệt lượng kế và tổn thất nhiệt. Tìm nhiệt độ ổn định của nước trong nhiệt lượng kế? Kết quả tính bằng\({\;^ \circ }{\rm{C}}\) và làm tròn đến một chữ số thập phân.
Quảng cáo
Trả lời:
Phương pháp:
- Tính nhiệt dung riêng trung bình của vật: \(\overline c = \frac{{{c_0} + {c_t}}}{2}\).
- Áp dụng phương trình cân bằng nhiệt.
Cách giải:
Nhiệt dung riêng trung bình khi nhiệt độ vật tăng từ 0 đến \(t\) là:
\(\overline c = \frac{{{c_0}\left( {1 + \alpha .0} \right) + {c_0}\left( {1 + \alpha t} \right)}}{2} = {c_0}\left( {1 + \frac{1}{2}\alpha t} \right)\)
\({Q_v} = {Q_n} \Rightarrow {m_0}\overline c t = 0,5.{m_0}{c_1}\left( {{t_{01}} - t} \right)\)
Thay số vào ta được:
\(1,3.10{\rm{\;}}.\left( {1 + \frac{1}{2}.0,012.{\rm{t}}} \right).{\rm{t}} = 0,5.4200.\left( {45 - {\rm{t}}} \right) \Rightarrow {\rm{t}} \approx 26,2\left( {{\;^ \circ }{\rm{C}}} \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
Áp dụng phương trình trạng thái khí lí tưởng: \(\frac{{pV}}{T} = \) const
Cách giải:
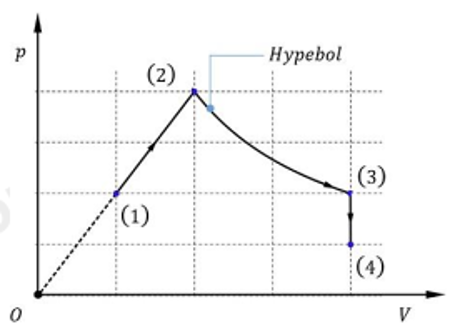
Áp dụng phương trình trạng thái khí lý tưởng ở trạng thái 1 và 4:
\(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_4}{V_4}}}{{{T_4}}} \Rightarrow \frac{{2.1}}{{300}} = \frac{{1.4}}{{{T_4}}}\)
\( \Rightarrow {T_4} = 600\left( {\rm{K}} \right)\)
Chọn C.
Lời giải
Phương pháp:
- Nhiệt lượng do ấm cung cấp: \(Q = P.\tau \)
- Nhiệt lượng cần cung cấp trong quá trình truyền nhiệt để làm thay đổi nhiệt độ: \(Q = mc{\rm{\Delta }}t\).
- Công suất của ấm: \(P = \frac{Q}{t}\)
Cách giải:
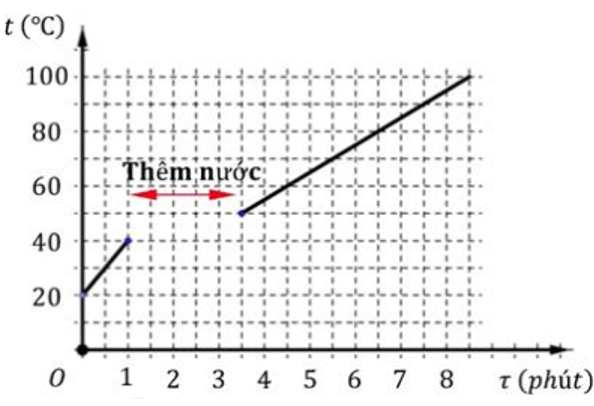
a) Nhiệt lượng do ấm cung cấp từ thời điểm ban đầu đến lúc nước bắt đầu sôi là:
\(Q = P.\tau = 2100.8,5.60 = 1071000\left( J \right) = 1071\left( {kJ} \right)\)
\( \to \) a sai.
b) Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{P{\tau _1} = {m_1}c\left( {{t_1} - {t_0}} \right)}\\{P\left( {{\tau _2} - {\tau _1}} \right) = {m_1}c\left( {{t_2} - {t_1}} \right) + {m_x}c\left( {{t_2} - {t_x}} \right)}\\{P\left( {{\tau _3} - {\tau _2}} \right) = \left( {{m_1} + {m_x}} \right).c\left( {100 - {t_2}} \right)}\end{array}} \right.\)
\( \Rightarrow \frac{P}{c} = \frac{{{m_1}\left( {40 - 20} \right)}}{{1.60}} = \frac{{{m_1}\left( {50 - 40} \right) + {m_x}\left( {50 - {t_x}} \right)}}{{\left( {3,5 - 1} \right).60}} = \frac{{\left( {{m_1} + {m_x}} \right)\left( {100 - 50} \right)}}{{5.60}}\)
\( \Rightarrow {m_1} = {m_x} \Rightarrow {t_x} = {10^ \circ }{\rm{C}}\)
\( \to {\rm{b}}\) đúng.
\( \to {\rm{c}}\) đúng.
d) Công suất của ấm:
\(P = \frac{{{m_1}c\left( {{t_1} - {t_0}} \right)}}{{{\tau _1}}} = \frac{{1,5.4200.\left( {40 - 20} \right)}}{{1.60}} = 2100\left( {\rm{W}} \right)\)
\( \to \) d sai.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. -20 J.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. tăng gấp bốn lần.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.