Để loại bỏ \(x\% \) chất gây ô nhiễm môi trường từ khí thải của một nhà máy, người ta ước tính chi phí (triệu đồng) cần bỏ ra được mô hình hoá bởi hàm số có dạng \(C\left( x \right) = \frac{{ax + b}}{{ - x + d}}\) (như hình vẽ), \(\left( {0 \le x < 100} \right).\) Tính chi phí chênh lệch (tỉ đồng) phải bỏ ra để loại bỏ \(90\% \) và loại bỏ \(99\% \) chất gây ô nhiễm từ khí thải của nhà máy.
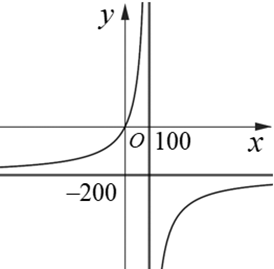
Để loại bỏ \(x\% \) chất gây ô nhiễm môi trường từ khí thải của một nhà máy, người ta ước tính chi phí (triệu đồng) cần bỏ ra được mô hình hoá bởi hàm số có dạng \(C\left( x \right) = \frac{{ax + b}}{{ - x + d}}\) (như hình vẽ), \(\left( {0 \le x < 100} \right).\) Tính chi phí chênh lệch (tỉ đồng) phải bỏ ra để loại bỏ \(90\% \) và loại bỏ \(99\% \) chất gây ô nhiễm từ khí thải của nhà máy.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Ta có \(C\left( x \right) = \frac{{ax + b}}{{ - x + d}} \cdot \) Từ đồ thị suy ra \(b = 0\,;d = 100\,;\,a = 200 \Rightarrow C\left( x \right) = \frac{{200x}}{{100 - x}} \cdot \)
Chi phí chênh lệch là \(\Delta C = \left| {C\left( {99} \right) - C\left( {90} \right)} \right| = \left| {\frac{{200 \cdot 99}}{{100 - 99}} - \frac{{200 \cdot 90}}{{100 - 90}}} \right| = 18\,000\) (triệu đồng) \( = 18\) (tỉ đồng).
Đáp án: 18.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \[M\left( {{x_0};{y_0}} \right) \in \left( C \right) \Rightarrow M\left( {{x_0};\frac{{x_0^2 + 4{x_0} + 5}}{{{x_0} + 2}}} \right)\].
Gọi \[\left( d \right)\] là khoảng cách từ \[M\] đến đường thẳng \[3x + y + 6 = 0\].
Ta có \[d = \frac{1}{{\sqrt {10} }}\left| {\frac{{4x_0^2 + 16{x_0} + 17}}{{{x_0} + 2}}} \right| = \frac{1}{{\sqrt {10} }}\left| {4\left( {{x_0} + 2} \right) + \frac{1}{{{x_0} + 2}}} \right| \ge \frac{4}{{\sqrt {10} }}\].
Đẳng thức xảy ra \[ \Leftrightarrow 4\left| {{x_0} + 2} \right| = \frac{1}{{\left| {{x_0} + 2} \right|}} \Leftrightarrow \left[ \begin{array}{l}{x_0} = \frac{{ - 3}}{2} \Rightarrow {y_0} = \frac{5}{2}\\{x_0} = \frac{{ - 5}}{2} \Rightarrow {y_0} = - \frac{5}{2}\end{array} \right.\].
Vậy có hai điểm thoả yêu cầu bài toán là \[{M_1}\left( {\frac{{ - 3}}{2};\frac{5}{2}} \right)\] và \[{M_2}\left( {\frac{{ - 5}}{2};\frac{{ - 5}}{2}} \right)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
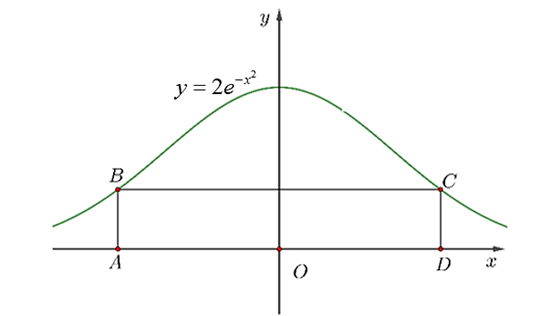
Giả sử điểm \(C\left( {x;2\,{{\rm{e}}^{ - {x^2}}}} \right)\) với \(x > 0\).
Diện tích của hình chữ nhật \(ABCD\) là \(f\left( x \right) = 4x \cdot {{\rm{e}}^{ - {x^2}}}\).
Ta có \(f'\left( x \right) = 4{{\rm{e}}^{ - {x^2}}} - 8{x^2}{{\rm{e}}^{ - {x^2}}}\)\( = 4{{\rm{e}}^{ - {x^2}}}\left( {1 - 2{x^2}} \right)\).
\(f'\left( x \right) = 0\) \( \Rightarrow \left[ \begin{array}{l}x = \frac{{\sqrt 2 }}{2}\,\,\,\,\,\left( n \right)\\x = - \frac{{\sqrt 2 }}{2}\,\,\,\,\,\,\left( l \right)\end{array} \right.\).
Bảng biến thiên
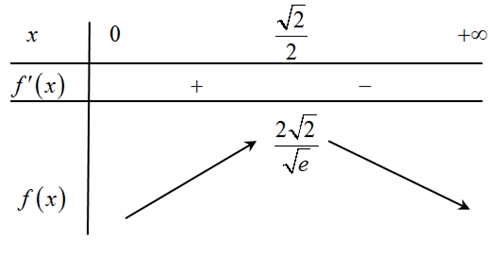
Vậy .
Câu 3
![Cho hàm số \[y = f\left( x \right)\] có đồ thị như hình. Phát biểu nào sau đây là đúng? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/08/blobid18-1756132927.png)
A. Đồ thị hàm số có đường tiệm cận đứng \[x = 1,\] đường tiệm cận ngang \[y = 2.\]
B. Đồ thị hàm số có đường tiệm cận đứng \[x = 2,\] đường tiệm cận ngang \[y = 1.\]
C. Đồ thị hàm số có đường tiệm cận đứng \[x = 2,\] đường tiệm cận ngang \[y = 0.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\left( { - 2\,; - 3} \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(2\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập