PHẦN II. TRẢ LỜI NGẮN
Anh Minh đầu tư số tiền bằng nhau vào hai lĩnh vực A và B. Biểu đồ dưới đây mô tả số tiền thu được mỗi tháng trong vòng 60 tháng theo mỗi lĩnh vực A và B.
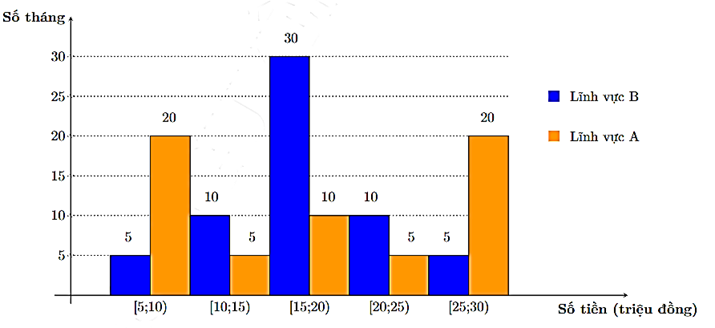
Hiệu độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào lĩnh vực A và B bằng bao nhiêu? (làm tròn kết quả đến hàng phần chục).
PHẦN II. TRẢ LỜI NGẮN
Anh Minh đầu tư số tiền bằng nhau vào hai lĩnh vực A và B. Biểu đồ dưới đây mô tả số tiền thu được mỗi tháng trong vòng 60 tháng theo mỗi lĩnh vực A và B.
Hiệu độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào lĩnh vực A và B bằng bao nhiêu? (làm tròn kết quả đến hàng phần chục).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có bảng tần số ghép nhóm sau:
|
[5; 10) |
[10; 15) |
[15; 20) |
[20; 25) |
[25; 30) |
|
|
Giá trị đại diện |
7,5 |
12,5 |
17,5 |
22,5 |
27,5 |
|
Lĩnh vực A |
20 |
5 |
10 |
5 |
20 |
|
Lĩnh vực B |
5 |
10 |
30 |
10 |
5 |
Ta có \(\overline {{x_A}} = \frac{{7,5.20 + 12,5.5 + 17,5.10 + 22,5.5 + 27,5.20}}{{20 + 5 + 10 + 5 + 20}} = 17,5\).
Phương sai: \(s_A^2 = \frac{{{{7,5}^2}.20 + {{12,5}^2}.5 + {{17,5}^2}.10 + {{22,5}^2}.5 + {{27,5}^2}.20}}{{20 + 5 + 10 + 5 + 20}} - {17,5^2} = \frac{{425}}{6}\).
Độ lệch chuẩn: \({s_A} = \sqrt {\frac{{425}}{6}} \).
\(\overline {{x_B}} = \frac{{7,5.5 + 12,5.10 + 17,5.30 + 22,5.10 + 27,5.5}}{{5 + 10 + 30 + 10 + 5}} = 17,5\).
Phương sai: \(s_B^2 = \frac{{{{7,5}^2}.5 + {{12,5}^2}.10 + {{17,5}^2}.30 + {{22,5}^2}.10 + {{27,5}^2}.5}}{{5 + 10 + 30 + 10 + 5}} - {17,5^2} = 25\).
Độ lệch chuẩn: sB = 5.
Hiệu độ lệch chuẩn: sA – sB \( = \sqrt {\frac{{425}}{6}} - 5 \approx 3,4\).
Trả lời: 3,4.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Nhóm |
Giá trị đại diện |
Tần số |
|
\[\left[ {36;38} \right)\] |
\[37\] |
\[9\] |
|
\[\left[ {38;40} \right)\] |
\[39\] |
\[15\] |
|
\[\left[ {40;42} \right)\] |
\[41\] |
\[25\] |
|
\[\left[ {42;44} \right)\] |
\[43\] |
\[30\] |
|
\[\left[ {44;46} \right)\] |
\[45\] |
\[21\] |
|
|
|
\[n = 100\] |
Số trung bình cộng của mẫu số liệu ghép nhóm là:
\[\overline x \, = \frac{{37.9 + 39.15 + 41.25 + 43.30 + 45.21}}{{100}} = 41,78\]
Độ lệch chuẩn của mẫu số liệu ghép nhóm là:
\[\begin{array}{l}s\, = \sqrt {\frac{1}{{100}}\left[ {9.{{\left( {37 - 41,78} \right)}^2} + 15.{{\left( {39 - 41,78} \right)}^2} + 25.{{\left( {41 - 41,78} \right)}^2} + 30.{{\left( {43 - 41,78} \right)}^2} + 21.{{\left( {45 - 41,78} \right)}^2}} \right]} \\ = 2,45\end{array}\]
Trả lời: 2,45.
Lời giải
|
Trọng lượng (kg) |
[4; 6) |
[6; 8) |
[8; 10) |
[10; 12) |
[12; 14) |
|
Giá trị đại diện |
5 |
7 |
9 |
11 |
13 |
|
Số quả |
6 |
12 |
19 |
9 |
4 |
Ta có \(\overline x = \frac{{5.6 + 7.12 + 9.19 + 11.9 + 13.4}}{{6 + 12 + 19 + 9 + 4}} = 8,72\).
Phương sai: \({s^2} = \frac{{{5^2}.6 + {7^2}.12 + {9^2}.19 + {{11}^2}.9 + {{13}^2}.4}}{{6 + 12 + 19 + 9 + 4}} - {8,72^2} = \frac{{3001}}{{625}}\).
Độ lệch chuẩn \(s = \sqrt {\frac{{3001}}{{625}}} \approx 2,19\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập