Một khí cầu có lỗ hở phía dưới để áp suất khí trong và ngoài khí cầu như nhau, khi chưa làm nóng không khí trong khí cầu có nhiệt độ bằng nhiệt độ bên ngoài là \({25^ \circ }{\rm{C}}\); để khí cầu có thể bay lên người ta làm nóng không khí trong khí cầu lên \({50^ \circ }{\rm{C}}\). So với số mol khí trong khí cầu ngay khi chưa làm nóng, phần trăm số mol khí đã thoát ra khí cầu gần đúng là

Quảng cáo
Trả lời:
Phương pháp:
Phương trình Clapeyron: \(pV = nRT \Rightarrow n \sim \frac{1}{T}\)
Cách giải:
Ta có: \(pV = nRT \Rightarrow n \sim \frac{1}{T}\)
\( \Rightarrow \frac{{{n_1} - {n_2}}}{{{n_1}}} = \frac{{\frac{1}{{{T_1}}} - \frac{1}{{{T_2}}}}}{{\frac{1}{{{T_1}}}}} = \frac{{\frac{1}{{25 + 273}} - \frac{1}{{50 + 273}}}}{{\frac{1}{{25 + 273}}}} \approx 0,077\)
\( \Rightarrow \frac{{{n_1} - {n_2}}}{{{n_1}}} \approx 8{\rm{\% }}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
- Áp dụng phương trình trạng thái khí lý tưởng.
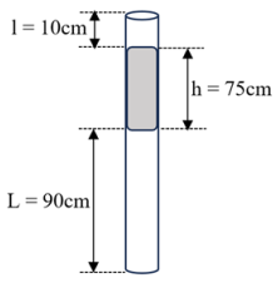
- Viết phương trình nhiệt độ theo chiều dài của cột thủy ngân còn lại. Sử dụng đạo hàm tìm nhiệt độ lớn nhất cần cung cấp để có thể đẩy được toàn bộ thủy ngân ra ngoài.
Cách giải:
a) Khi thủy ngân ở trạng thái cân bằng nên áp dụng định luật Charles ta có:
\(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow \frac{{L.S}}{{{T_1}}} = \frac{{{L_2}S}}{{{T_2}}} \Rightarrow \frac{{90}}{{ - 3 + 273}} = \frac{{{L_2}}}{{27 + 273}}\)
\( \Rightarrow {L_2} = 100\left( {{\rm{cm}}} \right)\)
\( \to \) a đúng.
b) Khi được làm nóng, cột thủy ngân sẽ dịch chuyển lên đầu trên do khí bên trong ống giãn nở đẩy thủy ngân đi lên.
\( \to \) b sai.
c) Giả sử thủy ngân trong ống còn \(x\left( {{\rm{cm}}} \right)\)
Áp suất của khí bên trong ống là: \(p = {p_0} + x\)
Áp dụng phương trình trạng thái khí:
\(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Rightarrow \frac{{\left( {{p_0} + x} \right)\left( {175 - x} \right).S}}{T} = \frac{{\left( {{p_0} + h} \right).L.S}}{{{T_1}}}\)
Thay số vào ta được:
\(\frac{{\left( {75 + x} \right)\left( {175 - x} \right)}}{T} = \frac{{\left( {75 + 75} \right).90}}{{ - 2 + 273}} = 50\)
\(T = \frac{{ - {x^2} + 100x + 13125}}{{50}}\)
\(T' = \frac{1}{{50}}\left( { - 2x + 100} \right) = 0 \Rightarrow x = 50\left( {{\rm{cm}}} \right)\)
\({T_{{\rm{max\;}}}} = \frac{{ - {{50}^2} + 100.50 + 13125}}{{50}} = 312,5\left( {\rm{K}} \right)\)
\( \to \) c sai.
d) Khi cột thủy ngân chưa trào ra ngoài thì quá trình biến đổi của khí trong ống không phải quá trình đẳng áp vì cột thủy ngân của nó có di chuyển.
Lời giải
Phương pháp:
- Lý thuyết về lực từ tác dụng lên dây dẫn.
- Bài toán cân dòng điện.
- Phương trình của đồ thị: \(m = {m_0} + kI\)
Cách giải:
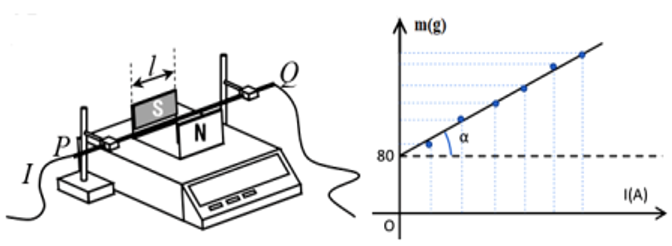
a) Từ đồ thị ta thấy, khi dòng điện tăng lên thì số chỉ trên cân tăng lên do đó lực từ tác dụng lên dây dẫn có chiều hướng lên, áp dụng quy tắc bàn tay trái xác định được dòng điện có chiều từ P đến Q.
\( \to \) a sai.
b) Không đủ dữ kiện để tính, 80 g là khối lượng của nam châm.
\( \to \) b sai.
c) Số chỉ của cân thay đổi là do lực từ tác dụng lên nam châm.
\( \to \) c sai.
d) Độ lớn của lực từ bằng trọng lượng của phần khối lượng tăng thêm:
\(\left( {m - {m_0}} \right)g = F \Rightarrow m = {m_0} + \frac{F}{g} = {m_0} + \frac{{B\ell }}{g}I\)
Mà phương trình của đồ thị có dạng: \(m = {m_0} + kI\) với hệ số \(k = {\rm{tan}}\alpha \).
\( \Rightarrow {\rm{tan}}\alpha = \frac{{B\ell }}{g} \Rightarrow {\rm{tan}}{28^ \circ } = \frac{{B.0,15}}{{9,8}} \Rightarrow B \approx 34,74\)
Vì khối lượng được tính theo đơn vị gam \( \Rightarrow B \approx 34,74\left( {{\rm{mT}}} \right)\)
Câu 3
A. \({50^ \circ }{\rm{C}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. có khối lượng riêng lớn.
B. có nhiệt dung riêng lớn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.