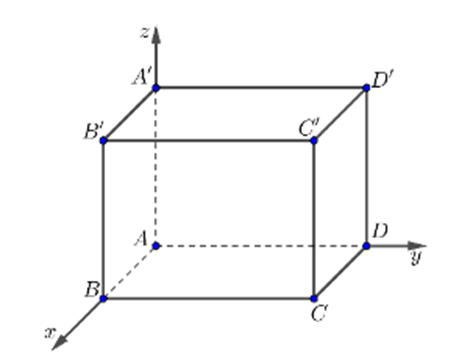
Trong không gian với hệ tọa độ Oxyz, cho hình lập phương ABCD.A'B'C'D' có độ dài cạnh bằng 1 như hình vẽ. Tọa độ \(\overrightarrow {AC} \) là:
(2; 0; 0).
(1; 1; 0).
(0; 0; 4).
(0; 1; 4).
Quảng cáo
Trả lời:
Đáp án đúng: B
Ta có A(0; 0; 0), C(1; 1; 0). Suy ra \(\overrightarrow {AC} = \left( {1;1;0} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
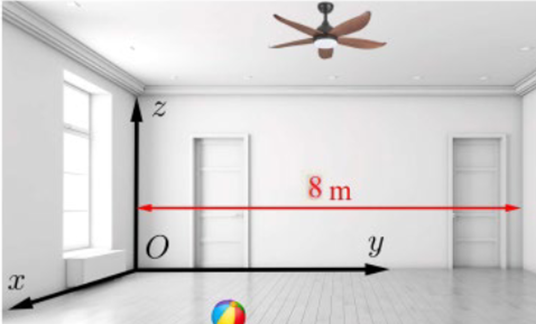
Căn phòng có chiều rộng 6m, chiều dài 8m, cao 4m. Cây quạt trần nằm ở vị trí tâm trần nhà. Do đó tọa độ của cây quạt trần là A(3; 4; 4).
Khi quạt rơi chạm sàn thì vị trí chạm sàn của cây quạt có tọa độ là A'(3; 4; 0).
Do đó a + b + c = 7.
Trả lời: 7.
Lời giải
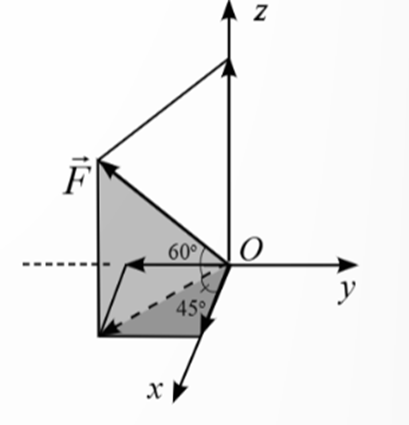
Đặt \(\overrightarrow F = \left( {x;y;z} \right)\), ta có:
x = 100.cos60°.cos45° = \(25\sqrt 2 \);
y = −100.cos60°.cos45° = \( - 25\sqrt 2 \);
z = 100.sin60° = \(50\sqrt 3 \).
Vậy \(\overrightarrow F = \left( {25\sqrt 2 ; - 25\sqrt 2 ;50\sqrt 3 } \right)\).
Suy ra a = 25; b = −25; c = 50. Do đó a + b + c = 50.
Trả lời: 50.
Câu 3
B'(8; 4; 10).
B'(6; 12; 0).
B'(10; 8; 6).
B'(13; 0; 17).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
(−4; −2; 9).
(4; 2; 9).
(−2; 4; −5).
(6; 2; −3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.