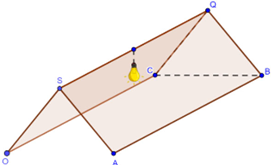
Người ta treo một chiếc đèn trang trí có trọng lượng 200 N lên trần nhà bằng ba sợi dây không dãn, bằng nhau tại ba điểm A, B, C tạo thành tam giác đều. Mỗi sợi dây tạo với mặt phẳng trần nhà một góc 30° đến được giữ ở trạng thái cân bằng (tham khảo hình vẽ). Hãy tính lực căng trong mỗi sợi dậy.
Quảng cáo
Trả lời:
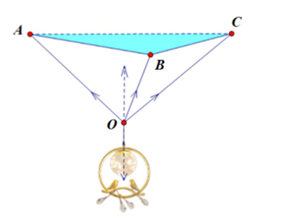
Lực căng trong mỗi dây sẽ bằng nhau.
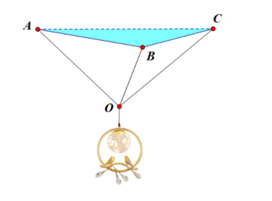
Gọi lực căng trong mỗi dây là \(\overrightarrow {{T_A}} ,\overrightarrow {{T_B}} ,\overrightarrow {{T_C}} \). Do đèn ở trạng thái cân bằng, các lực căng phải tạo ra một hợp lực bằng với trọng lượng của đèn, hướng thẳng lên trên.
Các lực căng \(\overrightarrow {{T_A}} ,\overrightarrow {{T_B}} ,\overrightarrow {{T_C}} \) đều phân tích được thành tổng hai thành phần lực thành phần ngang và thành phần đứng. Thành phần đứng của lực căng sẽ giúp cân bằng trọng lượng của đèn và thành phần ngang sẽ triệt tiêu lẫn nhau do tam giác đều đối xứng
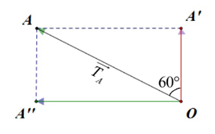
Mỗi dây tạo với mặt phẳng trần nhà góc 30°, do đó thành phần đứng của lực căng trong mỗi dây là: \(\left| {\overrightarrow {OA'} } \right| = \left| {\overrightarrow {OA} } \right|.\cos 60^\circ = \frac{1}{2}OA = \frac{1}{2}T\).
Tổng của ba thành phần đứng của lực căng phải cân bằng với trọng lượng của đèn nên suy ra
\(3T.\frac{1}{2} = 200 \Rightarrow T = \frac{{200}}{{\frac{3}{2}}} \approx 133\) (N).
Trả lời: 133.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
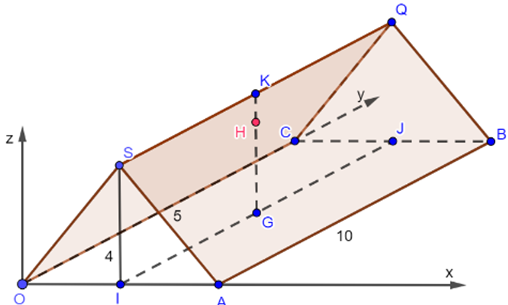
Gắn hệ trục tọa độ Oxyz như hình vẽ.
Gọi I, K lần lượt là trung điểm của OA, SQ.
\(OA = 2IA = 2\sqrt {{5^2} - {4^2}} = 6\).
Gọi H là vị trí chiếc đèn, KH = 30 cm = 0,3 m. Gọi G là giao điểm của hai đường chéo của hình chữ nhật OABC, suy ra HG = 4 – 0,3 = 3,7 m.
Do đó H(3; 5; 3,7).
Ta thấy OH = AH = CH = BH nên tổng chiều dài sợi dây màu xanh tối thiểu bạn An cần mua là 4OH.
Ta có \(\overrightarrow {OH} = \left( {3;5;3,7} \right) \Rightarrow 4OH = 4\sqrt {{3^2} + {5^2} + {{\left( {3,7} \right)}^2}} \approx 27,6\) m.
Trả lời: 27,6.
Lời giải
Vì hướng của con ong không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BM} \) cùng hướng.
Do vận tốc của con ong không đổi và thời gian bay từ A đến B bằng \(\frac{5}{3}\) thời gian bay từ B đến M nên ta có \(3\overrightarrow {AB} = 5\overrightarrow {BM} \).
Ta có \(3\overrightarrow {AB} = \left( {24;24;12} \right)\) và \(5\overrightarrow {BM} = \left( {5a - 50;5b - 60;5c - 25} \right)\).
Suy ra \(\left\{ \begin{array}{l}5a - 50 = 24\\5b - 60 = 24\\5c - 25 = 12\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{74}}{5}\\b = \frac{{84}}{5}\\c = \frac{{37}}{5}\end{array} \right.\).
Vậy 5a – b – c = 49,8.
Trả lời: 49,8.
Câu 3
A. \(\left( {0;0;\frac{1}{2}} \right)\).
(0; 2; 0).
\(\left( {\frac{1}{2};0;0} \right)\).
\(\left( {0;\frac{1}{2};0} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\(5\sqrt 2 \).
\(6\sqrt 2 \).
6.
12.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\(\left| {\overrightarrow {BD} } \right| = a\sqrt 2 \).
\(\left| {\overrightarrow {BD'} } \right| = a\sqrt 3 \).
\(\overrightarrow {AC} + \overrightarrow {A'C'} = \overrightarrow 0 \).
\(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.