Bạn Lan mang 150 000 đồng đi nhà sách để mua một số quyển tập và bút. Biết rằng giá một quyển tập là 8 000 đồng và giá của một cây bút là 6 000 đồng. Bạn Lan có thể mua được tối đa bao nhiêu quyển tập nếu bạn đã mua 10 cây bút.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi x là số quyển tập và y là số cây bút mà bạn Lan mua \(\left( {x,y \in \mathbb{N}} \right)\).
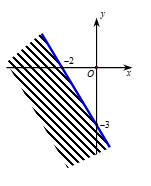
Bất phương trình biểu diễn số tập và bút có thể mua được phụ thuộc vào số tiền mang theo là \(8\,000x + 6\,000y \le 150\,000\).
Nếu bạn Lan đã mua 10 cây bút thì \(8\,000x + 6\,000 \cdot 10 \le 150\,000 \Leftrightarrow x \le 11,25\).
Vì \(x \in \mathbb{N}\) nên số quyển tập tối đa bạn Lan mua được là 11 quyển.
Đáp án: 11.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
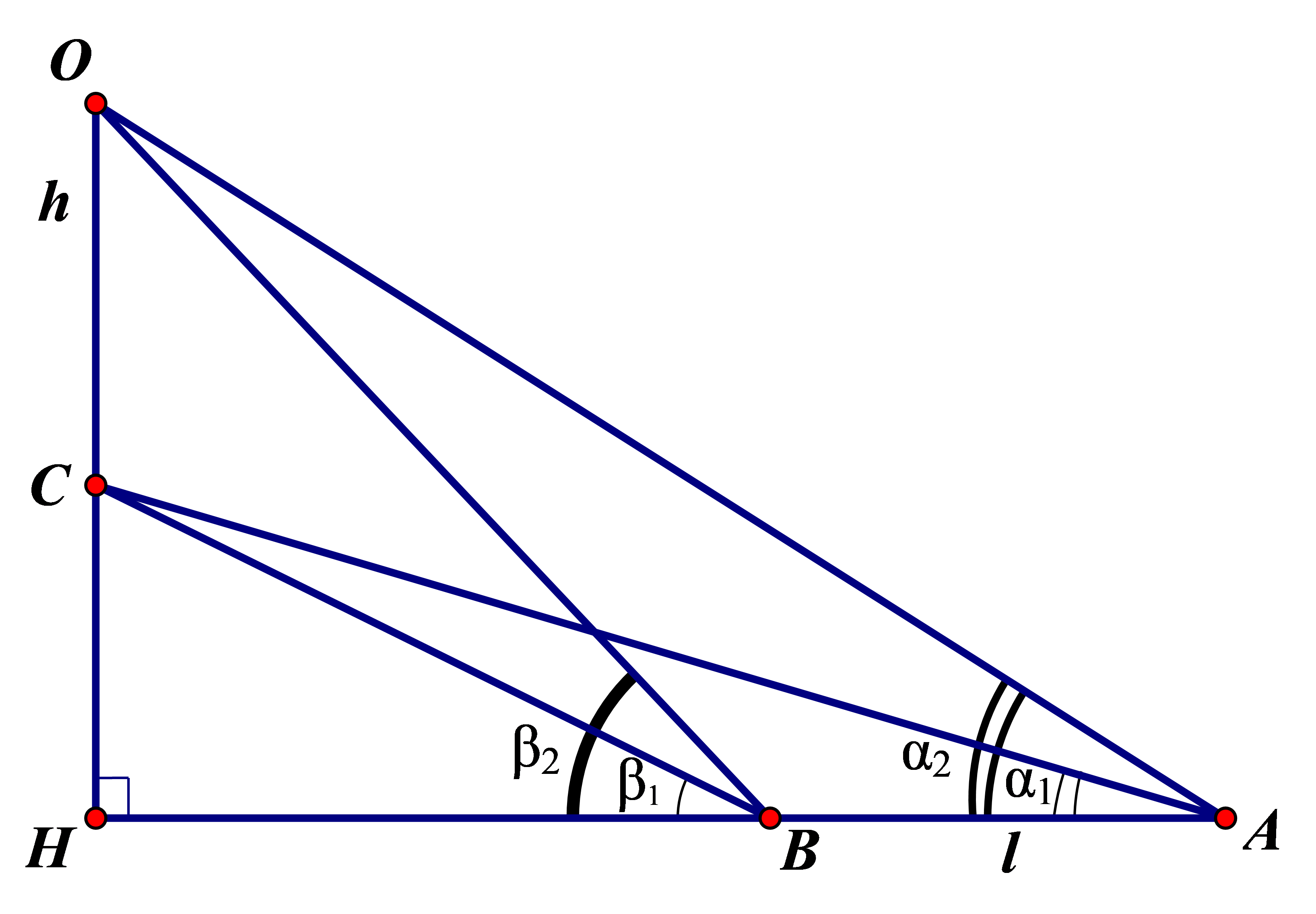
Có .
Áp dụng định lí sin vào , ta có: .
Xét vuông tại H, ta có: .
Có .
Áp dụng định lí sin vào , ta có: .
Xét vuông tại H, ta có: .
Vậy (m).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi số xe loại A cần thuê là \(x\,\,\left( {x \ge 0} \right)\).
Số xe loại B cần thuê là \(y\,\,\left( {y \ge 0} \right),x,y \in \mathbb{N}\).
Số người có thể chở tối đa là: \(20x + 10y\) (người).
Số tấn hàng có thể chở tối đa là: \(0,5x + 2y\) (tấn).
Theo đề bài, ta có:
- Cần chở ít nhất 100 người: \(20x + 10y \ge 100\).
- Cần chở ít nhất 6 tấn hàng: \(0,5x + 2y \ge 6\).
- Có 8 chiếc xe loại A và 6 chiếc xe loại B: \(x \le 8\), \(y \le 6\).
- Chi phí bỏ ra: \(F\left( {x;y} \right) = 4x + 3y\) (triệu đồng).
Ta có hệ bất phương trình: \[\left\{ {\begin{array}{*{20}{c}}{20x + 10y \ge 100}\\{0,5x + 2y \ge 6}\\{0 \le x \le 8}\\{0 \le y \le 6}\end{array}} \right.\]\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x + y \ge 10}\\{x + 4y \ge 12}\\{0 \le x \le 8}\\{0 \le y \le 6}\end{array}} \right.\] (I).
Bài toán trở thành tìm x, y thoả mãn hệ bất phương trình (I) để \(F\left( {x;y} \right) = 4x + 3y\) nhỏ nhất.
Miền nghiệm của hệ bất phương trình (I) là miền tứ giác ABCD kể cả biên.
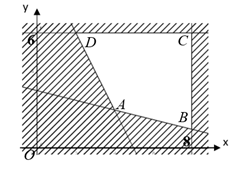
Toạ độ 4 đỉnh của miền nghiệm là: \(A\left( {4\,;\,2} \right)\), \(B\left( {8\,;\,1} \right)\), \(C\left( {8\,;\,6} \right)\), \(D\left( {2\,;\,6} \right)\).
Suy ra \(F\left( {x;y} \right) = 4x + 3y\) đạt GTNN bằng 22 tại\(\left( {4;2} \right)\).
Vậy doanh nghiệp nên thuê 4 xe loại A và 2 xe loại B để chi phí thấp nhất, và chi phí thấp nhất là 22 triệu đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập