Lớp 10E1 có 35 học sinh làm bài kiểm tra thường xuyên môn Toán. Đề bài gồm 3 bài toán. Sau khi kiểm tra cô giáo tổng hợp được kết quả như sau: có 12 học sinh chỉ giải được bài toán thứ nhất, 14 học sinh giải được bài toán thứ hai, 15 học sinh giải được bài toán thứ ba, 3 học sinh chỉ giải được bài toán thứ hai và thứ ba. Hỏi lớp 10E1 có bao nhiêu học sinh giải được cả 3 bài toán biết rằng mỗi học sinh đều làm được ít nhất một bài?
Quảng cáo
Trả lời:
Gọi x là số học sinh giải được cả 3 bài toán.
a là số học sinh chỉ làm được bài toán thứ nhất và thứ ba.
b là số học sinh chỉ làm được bài toán thứ nhất và thứ hai.
Khi đó:
Số học sinh chỉ làm được bài toán thứ ba là: 15 – a – x – 3 = 12 – x – a (học sinh).
Số học sinh chỉ làm được bài toán thứ hai là: 14 – b – x – 3 = 11 – x – b (học sinh).
Theo đề ta có phương trình: x + a + b + 3 + 12 + 12 – x – a + 11 – x – b = 35. Do đó x = 3.
Vậy có 3 học sinh giải được cả 3 bài toán.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số bộ sản phẩm loại \[I\] sản xuất trong một ngày là \[x\,\,,\,\,\,\left( {x \ge 0,x \in \mathbb{N}} \right)\].
Số bộ sản phẩm loại \[II\] sản xuất trong một ngày là \[y\,\,,\,\,\,\left( {y \ge 0,y \in \mathbb{N}} \right)\].
Số lãi thu được là \[L = 5x + 4y\] (triệu đồng).
Số giờ làm việc của máy là \[3x + 3y\] (giờ).
Số giờ làm việc của công nhân là \[2x + y\] (giờ).
Theo giả thiết: Một ngày máy làm việc không quá \[15\] giờ, nhân công làm việc không quá \[8\] giờ nên ta có hệ bất phương trình \[\left\{ \begin{array}{l}3x + 3y \le 15\\2x + y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\].
Miền nghiệm của hệ bất phương trình trên là
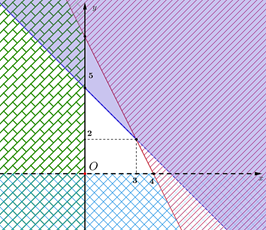
Tính các giá trị của biểu thức \[L = 5x + 4y\] tại các đỉnh của tứ giác là miền nghiệm của hệ bất phương trình trên ta được
\[\left( {x;y} \right) = \left( {0;0} \right) \Rightarrow L = 0\];
\[\left( {x;y} \right) = \left( {4;0} \right) \Rightarrow L = 20\];
\[\left( {x;y} \right) = \left( {3;2} \right) \Rightarrow L = 23\];
\[\left( {x;y} \right) = \left( {0;5} \right) \Rightarrow L = 20\].
Vậy số tiền lãi lớn nhất xưởng đó đạt được trong một ngày là \[23\] triệu đồng.
Lời giải
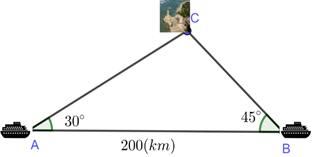
Tính được .
Áp dụng định lý sin vào tam giác ABC, ta có:
Thời gian tàu 1 chạy từ thành phố A đến đảo C là (giờ).
Thời gian tàu 2 chạy từ thành phố B đến đảo C là (giờ).
Ta có \({t_A} - {t_B} \approx 0,536\) (giờ) \( \approx 32\) (phút).
Khi đó, thời điểm xuất phát của tàu 2 là: 8 giờ 32 phút.
Vậy \(a = 8,\,b = 32.\) Suy ra \(a + b = 8 + 32 = 40\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.