Cho hình chữ nhật \(ABCD.\) Gọi \(M,\;N\) lần lượt là trung điểm của \(BC,\;AD.\) Biết rằng \(AM \bot MD,\;AM = 6\;{\rm{cm}},\) khi đó độ dài đoạn thẳng \(BN\) bằng bao nhiêu \({\rm{cm}}?\)
Cho hình chữ nhật \(ABCD.\) Gọi \(M,\;N\) lần lượt là trung điểm của \(BC,\;AD.\) Biết rằng \(AM \bot MD,\;AM = 6\;{\rm{cm}},\) khi đó độ dài đoạn thẳng \(BN\) bằng bao nhiêu \({\rm{cm}}?\)
Quảng cáo
Trả lời:
Đáp án: \(6\)
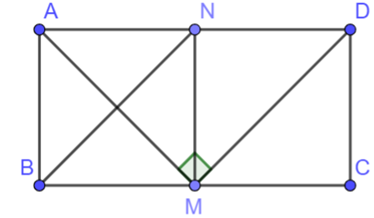
Vì tứ giác \(ABCD\) là hình chữ nhật nên \(\widehat {ABM} = \widehat {BAN} = \widehat C = 90^\circ ,\;AB = CD.\)
Vì \(M\) là trung điểm của \(BC\) nên \(BM = MC.\)
Tam giác \(ABM\) và tam giác \(DCM\) có: \(\widehat {ABM} = \widehat C = 90^\circ ,\;AB = CD,\;BM = MC.\)
Do đó, \(\Delta ABM = \Delta DCM\left( {c - g - c} \right)\) nên \(AM = DM.\)
Suy ra, \(\Delta ADM\) cân tại \(M.\) Do đó, \(MN\) là đường trung tuyến đồng thời là đường cao của \(\Delta ADM.\)
Do đó, \(\widehat {ANM} = 90^\circ .\)
Tứ giác \(ANMB\) có: \(\widehat {ABM} = \widehat {BAN} = \widehat {ANM} = 90^\circ \) nên tứ giác \(ANMB\) là hình chữ nhật \(\left( 1 \right).\)
Suy ra: \(\widehat {BMN} = 90^\circ \;\left( 2 \right).\)
Vì \(AM \bot MD\) nên \(\widehat {AMD} = 90^\circ .\)
Vì \(MN\) là đường trung tuyến đồng thời là đường phân giác của \(\Delta ADM\) nên
\(\widehat {AMN} = \frac{1}{2}\widehat {AMD} = \frac{1}{2} \cdot 90^\circ = 45^\circ \;\left( 3 \right).\)
Từ \(\left( 2 \right),\;\left( 3 \right)\) ta có: \(MA\) là tia phân giác của \(\widehat {BMN}\;\left( 4 \right).\)
Từ \(\left( 1 \right),\;\left( 4 \right)\) ta có: Tứ giác \(ANMB\) là hình vuông. Do đó, \(BN = AM = 6\;{\rm{cm}}.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng.
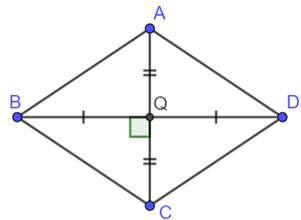
Tứ giác \(ABCD\) có: Hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(Q.\) Mà \(Q\) vừa là trung điểm của \(AC\) vừa là trung điểm của \(BD\) nên tứ giác \(ABCD\) là hình bình hành.
Lại có: \(AC \bot BD\) tại \(Q\) nên hình bình hành \(ABCD\) là hình thoi.
b) Đúng.
Vì tứ giác \(ABCD\) là hình thoi nên \(BC = AB = 4\;{\rm{cm}}{\rm{.}}\) Vậy \(BC = 4\;{\rm{cm}}{\rm{.}}\)
c) Sai.
Vì \(ABCD\) là hình thoi nên \(AC\) là tia phân giác của \(\widehat {BAD}.\) Do đó, \(\widehat {QAD} = \frac{1}{2}\widehat {BAD} = \frac{1}{2} \cdot 130^\circ = 65^\circ .\)
Tam giác \(QAD\) vuông tại \(Q\) nên \(\widehat {QAD} + \widehat {QDA} = 90^\circ .\) Do đó, \(\widehat {QDA} = 90^\circ - \widehat {QAD} = 90^\circ - 65^\circ = 25^\circ .\)
Vậy \(\widehat {ADB} = 25^\circ .\)
d) Đúng.
Vì tứ giác \(ABCD\) là hình thoi nên \(CA\) là tia phân giác của \(\widehat {BCD}.\)
Để hình thoi \(ABCD\) là hình vuông thì \(\widehat {BCD} = 90^\circ .\) Khi đó, \(\widehat {ACD} = \frac{1}{2}\widehat {BCD} = \frac{1}{2} \cdot 90^\circ = 45^\circ .\)
Vậy để tứ giác \(ABCD\) là hình vuông thì cần thêm điều kiện \(\widehat {ACD} = 45^\circ .\)
Câu 2
A. Hình chữ nhật.
Lời giải
Đáp án đúng là: B
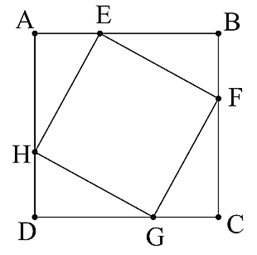
Vì có \(AB = BC = CD = DA\) và \(AE = BF = CG = DH\) nên
ta chứng minh được \(\Delta AEH = \Delta BFE = \Delta CGF = \Delta DHG\).
Suy ra \(HE = EF = FG = GH\) nên \(EFGH\) là hình thoi.
Mà \(\widehat {FEH} = 90^\circ \) nên \(EFGH\) là hình vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(AC = BD.\)
B. \(AC,{\rm{ }}BD\) giao nhau tại trung điểm mỗi đường.
C. \(AC \bot BD\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Hình chữ nhật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\widehat {ABC} = 80^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.