Cho ba số thực \(x,y,z \ne 0\) và \(x + y + z = 0\). Tính giá trị của biểu thức
\(T = \frac{{xy}}{{{x^2} + {y^2} - {z^2}}} + \frac{{yz}}{{{y^2} + {z^2} - {x^2}}} + \frac{{xz}}{{{z^2} + {x^2} - {y^2}}}\).
Cho ba số thực \(x,y,z \ne 0\) và \(x + y + z = 0\). Tính giá trị của biểu thức
\(T = \frac{{xy}}{{{x^2} + {y^2} - {z^2}}} + \frac{{yz}}{{{y^2} + {z^2} - {x^2}}} + \frac{{xz}}{{{z^2} + {x^2} - {y^2}}}\).
Quảng cáo
Trả lời:
Hướng dẫn giải
Từ \(x + y + z = 0\) suy ra \(z = - x - y;\,\,y = - x - z;\,\,x = - y - z.\)
Ta có: \(T = \frac{{xy}}{{{x^2} + {y^2} - {z^2}}} + \frac{{yz}}{{{y^2} + {z^2} - {x^2}}} + \frac{{xz}}{{{z^2} + {x^2} - {y^2}}}\)
\( = \frac{{xy}}{{{x^2} + {y^2} - {{\left( { - x - y} \right)}^2}}} + \frac{{yz}}{{{y^2} + {z^2} - {{\left( { - y - z} \right)}^2}}} + \frac{{xz}}{{{z^2} + {x^2} - {{\left( { - x - z} \right)}^2}}}\)
\( = \frac{{xy}}{{{x^2} + {y^2} - \left( {{x^2} + 2xy + {y^2}} \right)}} + \frac{{yz}}{{{y^2} + {z^2} - \left( {{y^2} + 2yz + {z^2}} \right)}} + \frac{{xz}}{{{z^2} + {x^2} - \left( {{z^2} + 2xz + {x^2}} \right)}}\)
\( = \frac{{xy}}{{ - 2xy}} + \frac{{yz}}{{ - 2yz}} + \frac{{xz}}{{ - 2xz}}\)
\( = \frac{1}{{ - 2}} + \frac{1}{{ - 2}} + \frac{1}{{ - 2}} = - \frac{3}{2}\)
Vậy \(T = - \frac{3}{2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
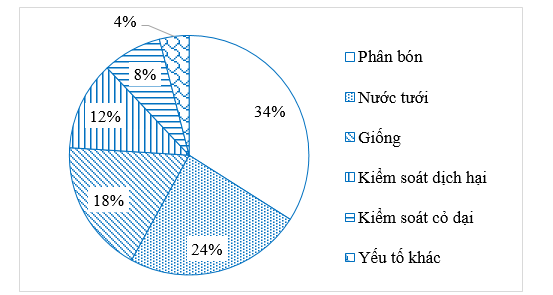
a) Trong các mặt hàng trên, sản phẩm được giảm giá nhiều nhất là áo sơ mi giảm \(35\% ,\) sản phẩm được giảm giá ít nhất là quần Jean giảm \(10\% .\)
b) Bạn An đã biểu diễn tỉ lệ giảm giá của các mặt hàng trên bằng biều đồ hình quạt tròn. Biểu đồ An sử dụng không phù hợp. Vì tỉ lệ phần trăm được giảm ở đây không phải tỉ lệ so với tổng thể.
c) An nên dùng biểu đồ cột để biểu diễn.
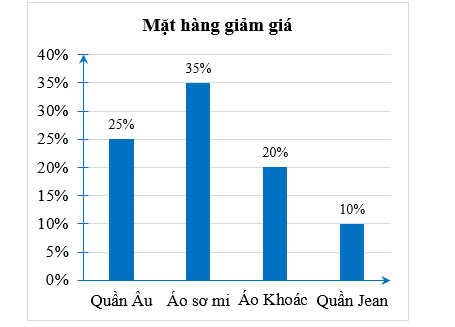
d) Áo sơ mi giảm \(35\% ,\) giá sau giảm là \(325\,\,000\) đồng. Do đó mỗi chiếc áo sơ mi nguyên giá sẽ là \(325\,\,000:\left( {100\% - 35\% } \right) = 500\,\,000\) (đồng).
Giá một chiếc quần Âu sau giảm là \(\frac{{1\,\,850\,\,000 - 325\,\,000 \cdot 2}}{4} = 300\,\,000\) (đồng).
Quần âu giảm giá \(25\% ,\) do đó mỗi chiếc quần âu nguyên giá sẽ là
\[300\,\,000:\left( {100\% - 25\% } \right) = 400\,\,000\] (đồng).
Lời giải
Hướng dẫn giải
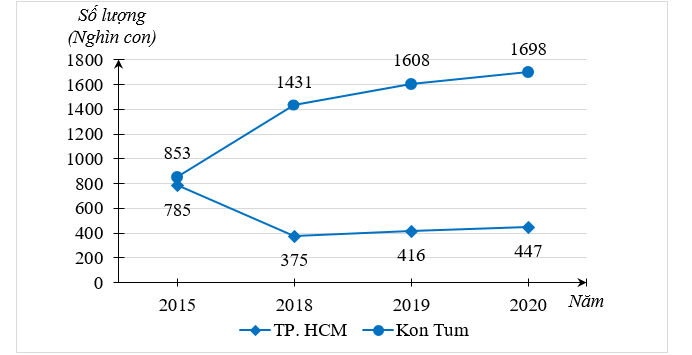
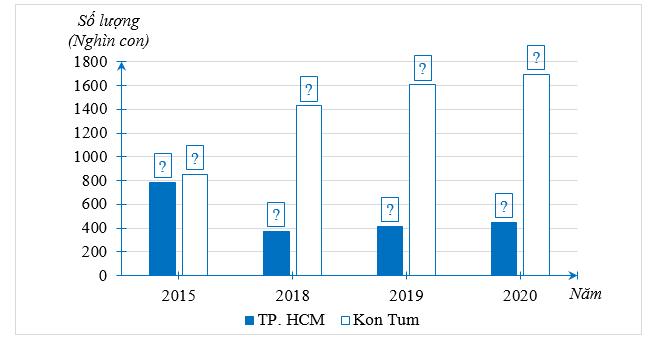
a) Ta hoàn thành được biểu đồ cột kép biểu diễn dữ liệu trong biểu đồ đoạn thẳng như sau:
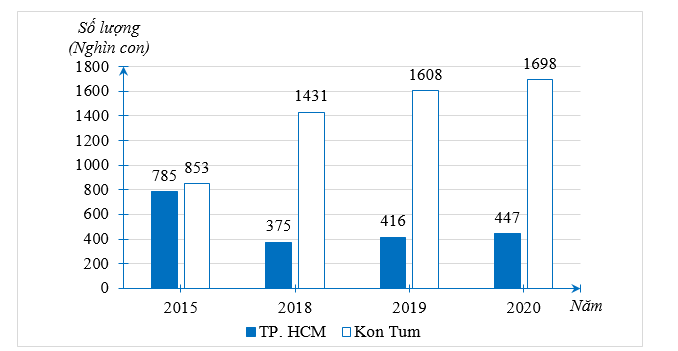
b) Trong năm 2020 lượng gia cầm ở Kon Tum nhiều nhất, là 1698 nghìn con.
c) Tổng số lượng gia cầm ở Kon Tum trong năm \[2015,\]\[2018,{\rm{ }}2019,{\rm{ }}2020\] là:
\(853 + 1\,\,431 + 1\,\,608 + 1\,\,698 = 5\,\,590\) (nghìn con).
Trong năm 2018, số lượng gia cầm ở TP. HCM \[(375\] nghìn con) ít hơn so với số lượng gia cầm ở Kon Tum \[(1{\rm{ }}431\] nghìn con) nên nhận định trên bài báo không chính xác.
d) Một vài giải pháp để tăng số lượng gia cầm ở Kon Tum trong những năm tới để đạt hiệu quả trong chăn nuôi:
⦁ Đẩy mạnh tuyên truyền, vận động nhân dân chăm sóc tốt đàn gia cầm hiện có;
⦁ Mạnh dạn đầu tư phát triển quy mô chăn nuôi, đa dạng các loại gia cầm;
⦁ Chú trọng việc lai tạo và cải thiện giống gia cầm địa phương;
⦁ Thường xuyên thực hiện vệ sinh tiêu độc khử trùng; …
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Hình dưới đây thể hiện số lượng học sinh tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của trường:
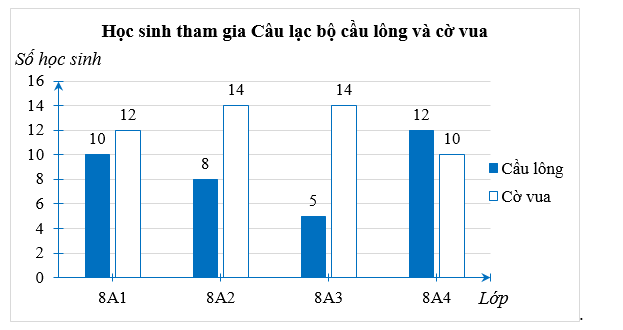
a) Lập bảng thống kê cho biểu đồ trên.
b) Cho biết sự khác nhau về việc tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của hai lớp 8A3 và 8A4.
c) Nếu lớp 8A1 có số lượng học sinh tham gia Câu lạc bộ cầu lông chiếm \(25\% \) tổng số học sinh cả lớp. Hãy tính xem lớp 8A1 có bao nhiêu học sinh.
d) Hãy so sánh tổng số học sinh tham gia Câu lạc bộ cầu lông và Câu lạc bộ cờ vua.
Hình dưới đây thể hiện số lượng học sinh tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của trường:

a) Lập bảng thống kê cho biểu đồ trên.
b) Cho biết sự khác nhau về việc tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của hai lớp 8A3 và 8A4.
c) Nếu lớp 8A1 có số lượng học sinh tham gia Câu lạc bộ cầu lông chiếm \(25\% \) tổng số học sinh cả lớp. Hãy tính xem lớp 8A1 có bao nhiêu học sinh.
d) Hãy so sánh tổng số học sinh tham gia Câu lạc bộ cầu lông và Câu lạc bộ cờ vua.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.