Cho hình vẽ bên. Biết \(\widehat {xOz} = 97^\circ ,\,\,\widehat {tOu} = 82^\circ \) và tia \(Oz\) là tia phân giác của góc \(\widehat {tOu}\).

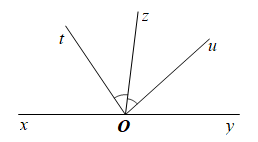
a) Vẽ lại hình và kể tên các cặp góc kề bù (không tính góc bẹt) có trong hình vẽ.

b) Tính số đo của góc \(\widehat {tOz},\,\,\widehat {tOy}\).

Hướng dẫn giải

Ta có \(VT = \left| {2x + 3} \right| + \left| {2x - 1} \right| = \left| {2x + 3} \right| + \left| {1 - 2x} \right| \ge \left| {2x + 3 + 1 - 2x} \right| = 4\).

Ta có \({\left( {x + 1} \right)^2} \ge 0\) suy ra \(3{\left( {x + 1} \right)^2} \ge 0\) nên \(3{\left( {x + 1} \right)^2} + 2 \ge 2\).

Do đó \(VP = \frac{8}{{3{{\left( {x + 1} \right)}^2} + 2}} \le 4\).

Ta thấy \(\left\{ \begin{array}{l}VT \ge 4\\VP \le 4\end{array} \right.\). Mà \(VT = VP\) nên \(VT = VP = 4\).

Khi đó \(\left\{ \begin{array}{l}x + 1 = 0\\\left( {2x + 3} \right)\left( {1 - 2x} \right) > 0\end{array} \right.\) nên \(x = - 1\).

Vậy \(x = - 1\).

Hướng dẫn giải

a) GT \(AB\parallel xy\), \(\widehat {BAI} = 45^\circ \), \(\widehat {AIF} = 105^\circ \). KL b) \(\widehat {FIx} = ?\); \(\widehat {FIy} = ?\) c) \[AB\parallel EF\] b) Vì \(AB\parallel xy\) nên \(\widehat {BAI} = \widehat {AIx} = 45^\circ \) (hai góc so le trong).

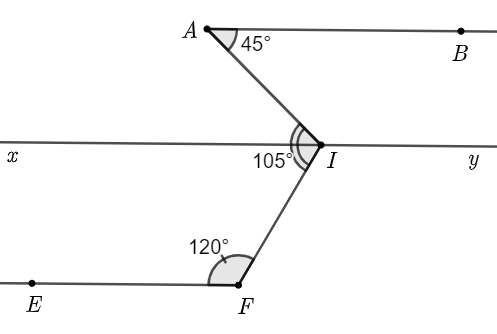Ta có \(\widehat {AIF} = \widehat {AIx} + \widehat {FIx}\).

Suy ra \(\widehat {FIx} = \widehat {AIF} - \widehat {AIx} = 105^\circ - 45^\circ = 60^\circ \).

Vì \(\widehat {FIx}\) và \(\widehat {FIy}\) là hai góc kề bù nên \(\widehat {FIx} + \widehat {FIy} = 180^\circ \).

Suy ra \(\widehat {FIy} = 180^\circ - \widehat {FIx} = 180^\circ - 60^\circ = 120^\circ \).

Vậy \(\widehat {FIx} = 60^\circ \); \(\widehat {FIy} = 120^\circ \).

c) Ta thấy \(\widehat {FIy} = \widehat {EFI} = 120^\circ \) mà \(\widehat {FIy}\) và \(\widehat {EFI}\) ở vị trí so le trong.

Do đó\[AB\parallel EF\].