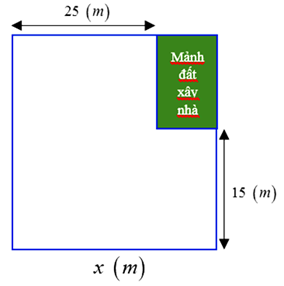
Thầy Việt dự định mua \[x\] quyển vở để trao thưởng cho những học sinh tiến bộ cuối năm học, mỗi quyển vở giá \[y\] đồng. Nhưng khi đến cửa hàng thầy Việt thấy giá vở đã giảm 2000 đồng mỗi quyển nên quyết định mua thêm 30 quyển.

a) Tìm đa thức biểu thị số tiền thầy Việt phải trả cho cửa hàng.

b) Hãy cho biết bậc của đa thức vừa tìm được ở câu a và tính số tiền thầy Việt phải trả nếu thầy mua 50 quyển vở và giá 1 quyển vở khi chưa giảm là 7000 đồng.

a) Xét tứ giác \(AMHN\) có \(\widehat {AMH} = \widehat {MAN} = \widehat {ANH} = {\rm{90^\circ }}\) Do đó tứ giác \[AMHN\] là hình chữ nhật. b) Tứ giác \[AMHN\] là hình chữ nhật nên \(AN = MH\) Mà \(PM = MH\)(do \[M\] là trung điểm của \[PH\,)\] nên\(AN = PM.\) Ta lại có \(AN\,{\rm{//}}\,PM\)(do \(AN \bot AB\,;PM \bot AB\,).\) Do đó tứ giác \(APMN\) là hình bình hành.

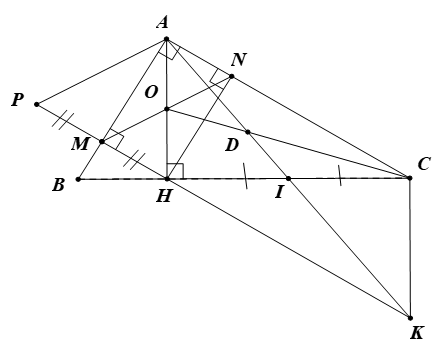c) Vì \(NC\parallel MK\) nên tứ giác \(MNCK\) là hình thang.

Tứ giác \(AHKC\) có hai đường chéo cắt nhau tại trung điểm \(I\) của mỗi đường nên là hình bình hành nên \(\widehat {HKC} = \widehat {HAC}\).         \(\left( 1 \right)\)

Tứ giác \(AMHN\) là hình chữ nhật.

Khi đó \(OA = ON = OM = OH\) nên \(\Delta OMH\) cân tại \(O\,.\)

Suy ra \(\widehat {OMH} = \widehat {OHM}\) mà \(\widehat {OAN} = \widehat {OHM}\) ( so le trong)

Do đó \(\widehat {OAN} = \widehat {OMH}\)       \(\left( 2 \right)\)

Từ \(\left( 1 \right),\,\,\left( 2 \right)\) suy ra \(\widehat {OMH} = \widehat {HKC}\).

Hình thang \(MNCK\) có hai góc kề một đáy bằng nhau nên là hình thang cân.

d) Vì \(\Delta AHC\) có hai đường trung tuyến \(AI,\,\,CO\) cắt nhau tại \(D\) nên \(D\) là trọng tâm nên

\(AD = \frac{2}{3}AI\) mà \(AI = \frac{1}{2}AK\).

Thay vào ta được \(AD = \frac{2}{3} \cdot \frac{1}{2}AK = \frac{1}{3}AK\) nên \(AK = 3AD\).

Hướng dẫn giải a) Do \(ABCD\) là hình bình hành nên \(AB = CD\) và \(AB\,{\rm{//}}\,CD.\) Lại có \[M,{\rm{ }}N\] lần lượt là trung điểm của \[AB\] và \[CD\] nên \(AM = BM = \frac{1}{2}AB\) và \(DN = CN = \frac{1}{2}CD.\) Do đó \(AM = BM = DN = CN\).

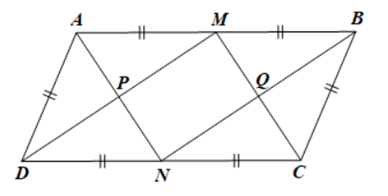Tứ giác \(DMBN\) có \(BM\,{\rm{//}}\,DN\) (do \(AB\,{\rm{//}}\,CD)\) và \(BM = DN\) nên \(DMBN\) là hình bình hành.

b) Xét tứ giác \(AMND\) có \(AM\,{\rm{//}}\,DN\) (do \(AB\,{\rm{//}}\,CD)\) và \(AM = DN\) nên \(AMND\) là hình bình hành.

Lại có \(AB = 2AD\) nên \(AD = \frac{1}{2}AB\), suy ra \(AM = AD\).

Hình bình hành \(AMND\) có \(AM = AD\) nên \(AMND\) là hình thoi

Suy ra đường chéo \(AN\) là đường phân giác của \(\widehat {DAM}\) hay \(\widehat {DAB}.\)

c) Chứng minh tương tự câu a, ta cũng có tứ giác \(AMCN\) là hình bình hành.

Suy ra \(AN\,{\rm{//}}\,CM\) hay \(PN\,{\rm{//}}\,QM\).

Do \(DMBN\) là hình bình hành nên \(DM\,{\rm{//}}\,BN\) hay \(PM\,{\rm{//}}\,QN\).

Tứ giác \[PMQN\] có \(PN\,{\rm{//}}\,QM\)và \(PM\,{\rm{//}}\,QN\) nên \[PMQN\] là hình bình hành.

Lại có \(AMND\) là hình thoi nên \(AN \bot DM\) hay \(\widehat {MPN} = 90^\circ \).

Do đó hình bình hành \[PMQN\] là hình chữ nhật.

Để \[PMQN\] là hình vuông thì \(PM = PN\,\,\,\left( * \right)\)

Mà \(PM = \frac{1}{2}DM\) và \(PN = \frac{1}{2}AN\) (do \(AMND\) là hình thoi nên \(P\) là trung điểm của hai đường chéo).

Do đó để \(\left( * \right)\) xảy ra thì \(DM = AN\) hay hình thoi \(AMND\) là hình vuông, khi đó \(\widehat {DAM} = 90^\circ .\)

Hình bình hành \(ABCD\) có \(\widehat {DAM} = 90^\circ \) thì sẽ trở thành hình chữ nhật.

Vậy để \[PMQN\] là hình vuông thì \(ABCD\) phải là hình chữ nhật.

Thật vậy, khi \(ABCD\) là hình vuông thì hình chữ nhật \[PMQN\] có \(PM = PN\) nên là hình vuông.