Máy chiếu xạ sử dụng nguồn phóng xạ $\beta^-$ cobalt $_{27}^{60}\mathrm{Co}$ với chu kì bán rã 5,27 năm (1 năm bằng 365 ngày) để điều trị ung thư. Nguồn phóng xạ trong máy sẽ cần được thay mới nếu như độ phóng xạ của nó giảm còn bằng một nửa độ phóng xạ ban đầu. Các phát biểu dưới đây là đúng hay sai?
a) Sản phẩm phân rã của cobalt $_{27}^{60}\mathrm{Co}$ là nickel $_{28}^{61}\mathrm{Ni}$.
b) Hằng số phóng xạ của cobalt $_{27}^{60}\mathrm{Co}$ là $\lambda=\dfrac{\ln 2}{T}\approx 4{,}17\cdot 10^{-9}\ \mathrm{s^{-1}}$.
c) Nguồn phóng xạ trong máy cần được thay mới sau mỗi năm.
d) Tại thời điểm thay nguồn phóng xạ, số hạt nhân $_{27}^{60}\mathrm{Co}$ còn lại trong nguồn bằng 50\% số hạt nhân $_{27}^{60}\mathrm{Co}$ ban đầu.

Máy chiếu xạ sử dụng nguồn phóng xạ $\beta^-$ cobalt $_{27}^{60}\mathrm{Co}$ với chu kì bán rã 5,27 năm (1 năm bằng 365 ngày) để điều trị ung thư. Nguồn phóng xạ trong máy sẽ cần được thay mới nếu như độ phóng xạ của nó giảm còn bằng một nửa độ phóng xạ ban đầu. Các phát biểu dưới đây là đúng hay sai?
a) Sản phẩm phân rã của cobalt $_{27}^{60}\mathrm{Co}$ là nickel $_{28}^{61}\mathrm{Ni}$.
b) Hằng số phóng xạ của cobalt $_{27}^{60}\mathrm{Co}$ là $\lambda=\dfrac{\ln 2}{T}\approx 4{,}17\cdot 10^{-9}\ \mathrm{s^{-1}}$.
c) Nguồn phóng xạ trong máy cần được thay mới sau mỗi năm.
d) Tại thời điểm thay nguồn phóng xạ, số hạt nhân $_{27}^{60}\mathrm{Co}$ còn lại trong nguồn bằng 50\% số hạt nhân $_{27}^{60}\mathrm{Co}$ ban đầu.

Quảng cáo
Trả lời:
|
|
Nội dung |
Đúng |
Sai |
|
a |
Sản phẩm phân rã của cobalt $_{27}^{60}\mathrm{Co}$ là nickel $_{28}^{61}\mathrm{Ni}$. |
|
S |
|
b |
Hằng số phóng xạ của cobalt $_{27}^{60}\mathrm{Co}$ là $\lambda=\dfrac{\ln 2}{T}\approx 4{,}17\cdot 10^{-9}\ \mathrm{s^{-1}}$. |
Đ |
|
|
c |
Nguồn phóng xạ trong máy cần được thay mới sau mỗi năm. |
|
S |
|
d |
Tại thời điểm thay nguồn phóng xạ, số hạt nhân $_{27}^{60}\mathrm{Co}$ còn lại trong nguồn bằng 50% số hạt nhân $_{27}^{60}\mathrm{Co}$ ban đầu. |
Đ |
|
a) Phản ứng phân hạch của Cobalt:
\[
{}_{27}^{60}\mathrm{Co} \rightarrow {}_{28}^{60}\mathrm{Ni} + {}_{-1}^{0}\mathrm{e} + \bar{\nu}_e
\]
b) Hằng số phóng xạ của cobalt $_{27}^{60}\mathrm{Co}$ là
\[
\lambda=\frac{\ln 2}{T}=\frac{\ln 2}{5{,}27\cdot 365\cdot 24\cdot 3600}\approx 4{,}17\cdot 10^{-9}\ \mathrm{s^{-1}}.
\]
c) Sau khoảng thời gian $t=T=5{,}27$ năm, độ phóng xạ của nguồn phóng xạ giảm 50%.
Vậy cứ sau 5,27 năm, nguồn phóng xạ trong máy cần được thay mới.
d) Khi độ phóng xạ bằng 50% độ phóng xạ ban đầu thì số hạt nhân của chất phóng xạ tại thời điểm đó cũng bằng 50% số hạt nhân ban đầu của chất phóng xạ.
\[
H_t=\lambda N_t;\quad H_0=\lambda N_0 \Rightarrow \frac{H_t}{H_0}=\frac{N_t}{N_0}.
\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
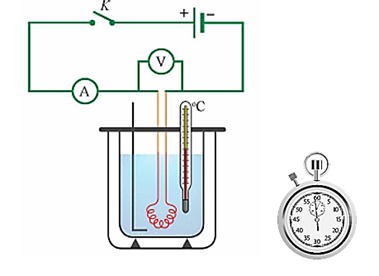
Nhiệt lượng Q toả ra trên dây nung được xác định bằng biểu thức $Q = U \cdot I \cdot t$. |
Đ |
|
|
b |
Trong quá trình làm thí nghiệm, học sinh dùng đũa khuấy nước nhẹ nhàng và liên tục để nhiệt lượng nước tỏa ra môi trường xung quanh một cách đều đặn. |
|
S |
|
c |
Nhiệt lượng nước cần thu vào để nhiệt độ tăng thêm $\Delta T$ (K) là $Q = m \cdot c \cdot \Delta T$. |
Đ |
|
|
d |
Nhiệt dung riêng của nước thu được từ thí nghiệm trên (làm tròn đến hàng đơn vị) xấp xỉ bằng 4200 J/(kg.K). |
|
S |
a) Theo định luật Joule – Lenxơ, nhiệt lượng tỏa ra trên đoạn dây dẫn có điện trở R là:
\[
Q = I^2 \cdot R \cdot t
\]
Mà $I = \dfrac{U}{R}$ (Định luật Ôm)
Suy ra: $Q = U \cdot I \cdot t$.
b) Trong quá trình làm thí nghiệm, học sinh dùng đũa khuấy nước nhẹ nhàng và liên tục để nhiệt lượng do dây nung tỏa ra được truyền đều cho lượng nước trong nhiệt lượng kế.
c) Đổi 2 phút 36 giây = 156 giây; 150 g = 0,15 kg
Do bỏ qua nhiệt lượng mà bình nhiệt lượng kế và đũa khuấy thu vào; bỏ qua nhiệt lượng dây nung tỏa ra môi trường không khí nên nhiệt lượng dây nung tỏa ra bằng nhiệt lượng nước thu vào.
\[
U \cdot I \cdot t = m \cdot c \cdot \Delta T
\;\;\Leftrightarrow\;\;
c = \frac{U \cdot I \cdot t}{m \cdot \Delta T}
= \frac{3{,}2 \cdot 2{,}5 \cdot 157}{0{,}15 \cdot (34 - 32)}
\approx 4187\ \mathrm{J/(kg\cdot K)}.
\]
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
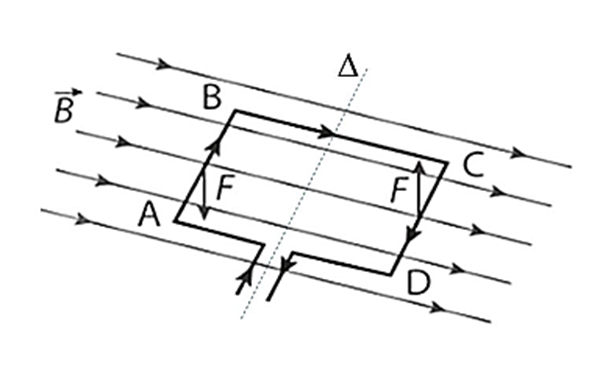
Mỗi cạnh AB và CD chịu tác dụng của lực từ $\vec{F}$ có độ lớn là F = 1,5 N. |
|
S |
|
b |
Lực từ tác dụng lên đoạn dây AB và CD có phương thẳng đứng. |
|
S |
|
c |
Moment ngẫu lực tác dụng lên khung dây có độ lớn là $M = F\cdot d = 12\cdot 10^{-4}\ \mathrm{N\cdot m}$. |
Đ |
|
|
d |
Lực từ tác dụng lên hai đoạn dây AB và CD là ngẫu lực làm cho khung dây quay quanh trục Δ. |
Đ |
|
a) Đổi 5 cm = 0,05 m; 8 cm = 0,08 m.
Mỗi cạnh AB và CD chịu tác dụng của lực từ có độ lớn là:
\[
F = B\cdot I \cdot l \cdot \sin(\vec{B};\vec{I})
= 0{,}15 \cdot 2 \cdot 0{,}05 \cdot \sin 90^\circ
= 0{,}015\ \mathrm{N}.
\]
Nên F = 1,5 N là sai.
b) Lực từ tác dụng lên đoạn dây AB và CD có phương vuông góc với mặt phẳng chứa đoạn dây dẫn mang dòng điện và vectơ cảm ứng từ, không phải phương thẳng đứng.
c) Moment ngẫu lực tác dụng lên khung dây có độ lớn là
\[
M = F\cdot d = 0{,}015 \cdot 0{,}08 = 12\cdot 10^{-4}\ \mathrm{N\cdot m}.
\]
d) Lực từ tác dụng lên hai đoạn dây AB và CD cùng phương, ngược chiều, cùng độ lớn và tác dụng lên khung dây ABCD nên chúng là ngẫu lực. Và ngẫu lực có tác dụng làm quay khung dây quanh trục Δ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
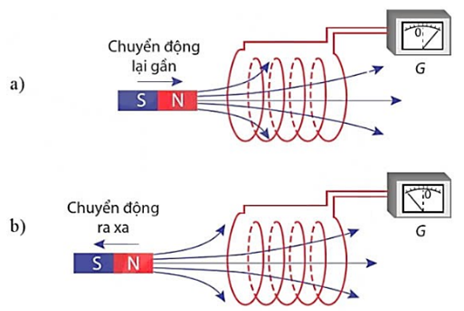
A. có độ lớn tăng lên.
B. có độ lớn giảm đi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.