Một bình cầu thể tích $V=9\,\text{lít}=9\cdot10^{-3}\,\text{m}^3$ chứa $n=2$ mol khí lí tưởng. Van bảo hiểm là một xi lanh có pít tông diện tích $S=40\,\text{cm}^2=4{,}0\cdot10^{-3}\,\text{m}^2$, giữ bằng lò xo độ cứng $k=100\,\text{N/m}$.
Khi $t_1=27^\circ\mathrm{C}$ ($T_1=300\,\text{K}$) pít tông ở cách lỗ thoát một đoạn $\ell=8\,\text{cm}=0{,}08\,\text{m}$. Lò xo luôn bị nén. Hỏi nhiệt độ $t_2$ khi khí bắt đầu thoát ra?
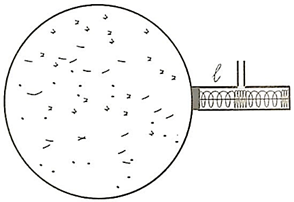
Khi $t_1=27^\circ\mathrm{C}$ ($T_1=300\,\text{K}$) pít tông ở cách lỗ thoát một đoạn $\ell=8\,\text{cm}=0{,}08\,\text{m}$. Lò xo luôn bị nén. Hỏi nhiệt độ $t_2$ khi khí bắt đầu thoát ra?

Quảng cáo
Trả lời:
Ở nhiệt độ t_1, lực F_1 do khí trong bình tác dụng lên pít tông bằng tổng lực đàn hồi F_{đh1} của lò xo và áp lực khí quyển F_{kq}:
\[
F_1 = F_{đh1} + F_{kq} \tag{1}
\]
Ở nhiệt độ t_2, lực F_2 do khí tác dụng lên pít tông bằng tổng lực đàn hồi F_{đh2} của lò xo và áp lực khí quyển F_{kq}:
\[
F_2 = F_{đh2} + F_{kq} \tag{2}
\]
Từ (1) và (2):
\[
F_2 - F_1 = F_{đh2} - F_{đh1} = k\,\ell \quad (*)
\]
Áp dụng phương trình Clapeyron cho trạng thái đầu:
\[
p_1 V = nRT_1 \;\Rightarrow\; p_1 = \frac{nRT_1}{V}
\]
Suy ra
\[
F_1 = p_1 S = \frac{nRT_1}{V}\,S \tag{3}
\]
Cho trạng thái sau:
\[
p_2 V = nRT_2 \;\Rightarrow\; p_2 = \frac{nRT_2}{V}
\]
Suy ra
\[
F_2 = p_2 S = \frac{nRT_2}{V}\,S \tag{4}
\]
Thế (3) và (4) vào (*):
\[
\frac{nRT_2}{V}\,S - \frac{nRT_1}{V}\,S = k\,\ell
\]
\[
T_2 = T_1 + \frac{k\,\ell\,V}{nRS}
\]
Vì n = 2 mol nên
\[
T_2 = T_1 + \frac{k\,\ell\,V}{2RS}
\]
Suy ra theo độ C (độ tăng nhiệt giống nhau trên thang K và ^\circ C):
\[
t_2 = t_1 + \frac{k\,\ell\,V}{2RS}
\]
Thay số: \(k=100\,\mathrm{N/m},\ \ell=8\ \mathrm{cm}=8\times10^{-2}\ \mathrm{m},\ V=9\,\mathrm{l}=9\times10^{-3}\ \mathrm{m^3},\ S=40\,\mathrm{cm^2}=40\times10^{-4}\ \mathrm{m^2},\ R=8{,}31\,\mathrm{J/(mol\,K)}\)
\[
t_2 = 27 + \frac{100\cdot 8\times10^{-2}\cdot 9\times10^{-3}}{2\cdot 8{,}31\cdot 40\times10^{-4}}
\approx 29^\circ\mathrm{C}.
\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
Khối khí nở ra và đẩy pít tông chuyển động thẳng nhanh dần đều. |
Đ |
|
|
b |
Công mà khối khí đã thực hiện để pít tông di chuyển 5 cm bằng 1,05 J. |
|
S |
|
c |
Nếu nhiệt lượng đã cung cấp cho khối khí để đẩy pít tông di chuyển 5 cm như trên là 30 J thì độ biến thiên nội năng của khối khí là 16,45 J. |
Đ |
|
|
d |
Nếu tiếp tục cung cấp nhiệt cho khối khí thì pít tông sẽ di chuyển tiếp đến miệng xi lanh. Trong quá trình đó, nhiệt độ của khối khí tăng gấp 2 lần. |
|
S |
a) ĐÚNG
b) SAI
Lực tác dụng lên pít tông:
\[
\vec F + \vec F_0 + \vec F_{\mathrm{ms}} = m\,\vec a
\]
Chọn chiều dương là chiều chuyển động nên:
\[
F - F_0 - F_{\mathrm{ms}} = m a
\]
\[
F = m a + F_0 + F_{\mathrm{ms}} = m a + p_0 S + F_{\mathrm{ms}}
\]
\[
F = 0{,}2\cdot 5 + 10^5 \cdot 25\cdot 10^{-4} + 20 = 271
\]
Công khí thực hiện khi pít tông đi 5 cm:
\[
A = F\,s\,\cos 0^\circ = 271 \cdot 0{,}05 = 13{,}55\ \mathrm{J}
\]
c) ĐÚNG
Định luật I nhiệt động lực học:
\[
\Delta U = Q - A = 30 - 13{,}55 = 16{,}45\ \mathrm{J}
\]
d) SAI
Khí được nung đều, pít tông luôn chuyển động với gia tốc không đổi và áp suất khí coi như không đổi (xấp xỉ đẳng áp). Khi pít tông tiếp tục đi đến miệng ống xi lanh:
\[
\frac{V_2}{V_1} = \frac{(15+5)}{(15)} = \frac{T_2}{T_1} \Rightarrow \frac{T_2}{T_1} = 1{,}5
\]
Nhiệt độ tăng 1,5 lần (không phải gấp 2 lần).
Câu 2
A. Sự thăng hoa.
B. Sự nóng chảy.
C. Sự ngưng tụ.
D. Sự hóa hơi.
Lời giải
Đáp án đúng là D
Hiện tượng tạo khói được hình thành do Nitrogen ở dạng lỏng hóa hơi. Khi làm kem, người bán hàng thêm một lượng Nitrogen ở dạng lỏng vào để giúp kem nhanh đông đặc và đồng thời hóa hơi tạo khói.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. $\tfrac{8}{3}\cdot 10^{-6}$ N.
B. 0 N.
C. $\tfrac{16}{3}\cdot 10^{-6}$ N.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
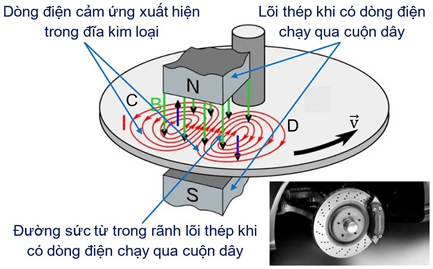
Câu 6
A. Phanh điện từ hoạt động dựa trên tương tác không tiếp xúc.
B. Phanh điện từ hoạt động dựa trên tương tác giữa nam châm và dòng điện cảm ứng.
C. Phanh điện từ chỉ hoạt động khi từ trường của nam châm thay đổi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.