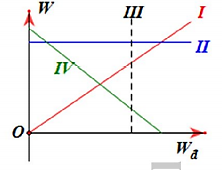
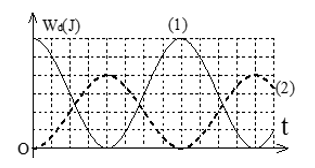
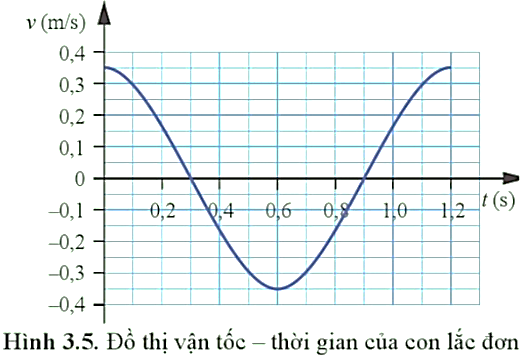
PHẦN III. Câu trắc nghiệm trả lời ngắn

Một con lắc đơn có chiều dài \[l = 1,2\]m dao động nhỏ với tần số góc bằng 2,86 rad/s tại nơi có gia tốc trọng trường \[g\]. Giá trị của \[g\] tại đó bằng bao nhiêu m/s² ? (Làm tròn đến chữ số thập phân thứ 2 sau dấu phẩy)

Phát biểu

Đúng

Sai

a

Ta có: A = 0,05cm; ꞷ = 20 rad/s

 Cơ năng \(W = \,40J\)

b

Biểu thức động năng và thế năng lần lượt là:

; \({W_t} = 0,1{\cos ^2}(20t)(J)\)

c

Thế năng của con lắc tại thời điểm 2 giây là: \({W_t} = 17,79J\)

d

Khi vật ở vị trí +A, ta có W_đmax = W: \({v_{max}} = 20\sqrt {10} \) cm/s             

Phát biểu

Đúng

Sai

a

Con lắc đơn dao động điều hòa với tần số góc \(\omega = \frac{{7\pi }}{{10}}\left( {rad/s} \right)\)

b

Cơ năng của vật được bảo toàn nên ở vị trí thấp nhất W = 0,3 J

c

Khi vật ở vị trí thấp nhất: W_đ = 0

d

Vận tốc của con lắc đơn khi qua vị trí thấp nhất theo chiều dương là: \({v_{max}} = \;0,77\;\;m/s\)

Phát biểu

Đúng

Sai

a

Từ đồ thị ta có: \(\omega = \frac{{5\pi }}{3}(rad/s)\)

b

Phương trình vận tốc: \(v = 0,35\cos \left( {\frac{{5\pi }}{3}t} \right)\left( {m/s} \right)\)

c

Cơ năng của vật: W = \(4,{9.10^{ - 3}}J\)

d

Tại thời điểm 0,4s thế năng của vật: \[{W_t} = 9,{1875.10^{ - 3}}J\]      

Phát biểu

Đúng

Sai

a

Trong quá trình dao động, cơ năng của vật là được bảo toàn.

b

Khi vật chuyển động từ vị trí cân bằng đến biên dương, thế năng tăng dần đều.

c

Vận tốc cực đại của vật là v_max = 20 cm/s.

d

Tại vị trí cân bằng, động năng của vật đạt cực đại: W_dmax = 200 mJ.