Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn điều kiện \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1\) và \(\overrightarrow a .\overrightarrow b = 3.\) Độ dài vectơ \(3\overrightarrow a + 5\overrightarrow b \) là
Quảng cáo
Trả lời:
Chọn B
\({\left( {3\overrightarrow a + 5\overrightarrow b } \right)^2} = 9{\overrightarrow a ^2} + 30\overrightarrow a \overrightarrow b + 25{\overrightarrow b ^2}\) \( = 9 + 90 + 25 = 124\)\( \Rightarrow \left| {3\overrightarrow a + 5\overrightarrow b } \right| = \sqrt {124} \).
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
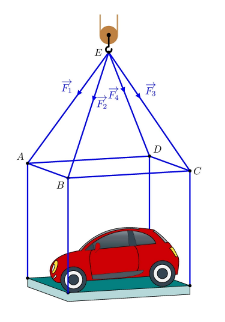
Lấy các điểm \(M,N,P,Q\)lần lượt trên các tia \(EA,EB,EC,ED\) sao cho
\(\overrightarrow {EM} = \overrightarrow {{F_1}} ,\overrightarrow {EN} = \overrightarrow {{F_2}} ,\overrightarrow {EP} = \overrightarrow {{F_3}} ,\overrightarrow {EQ} = \overrightarrow {{F_4}} {\rm{. }}\)
Do các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} ,\overrightarrow {{F_4}} \) đều có cường độ là \(4700\;{\rm{N}}\) nên \(EM = EN = EP = EQ = 4700\).
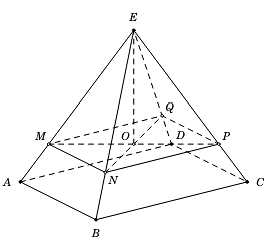
a) Sai. Ta có: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {EM} + \overrightarrow {EN} = 2\overrightarrow {EH} \), với \(H\) là trung điểm của \(MN\).
\(\overrightarrow {{F_3}} + \overrightarrow {{F_4}} = \overrightarrow {EP} + \overrightarrow {EQ} = 2\overrightarrow {EK} \), với \(K\) là trung điểm của \[PQ\] suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \ne \overrightarrow {{F_3}} + \overrightarrow {{F_4}} \).
b) Đúng. Ta có \(\overrightarrow {{F_1}} + \overrightarrow {{F_3}} = \overrightarrow {EM} + \overrightarrow {EP} = 2\overrightarrow {EO} \), với \(O\) là trung điểm của \(MP\).
\(\overrightarrow {{F_2}} + \overrightarrow {{F_4}} = \overrightarrow {EN} + \overrightarrow {EQ} = 2\overrightarrow {EO} ,\) với \(O\) là trung điểm của \[MP\] suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_3}} = \overrightarrow {{F_2}} + \overrightarrow {{F_4}} \).
c) Đúng. \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_3}} } \right| = |2\overrightarrow {EO} | = 2EO\). Theo giả thiết, góc giữa \(EA\)với \(\left( {ABCD} \right)\) bằng \(60^\circ \) nên góc giữa \(EM\)với \(\left( {MNPQ} \right)\) cũng bằng \(60^\circ \) hay \(\widehat {SMO} = 60^\circ \).
Xét \(\Delta EMO\) có \(EM = 4700,\widehat {\,SMO} = 60^\circ \) suy ra \(EO = EM\sin 60^\circ = 2350\sqrt 3 \).
d) Đúng. Từ đây ta tính được \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_3}} } \right| = 2EO = 8141\;{\rm{N}}\).
Lời giải
a) Đúng. Theo công thức vì \[G\] là trọng tâm tứ diện \[ABCD \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \].
b) Đúng. Ta có:
\[\overrightarrow {OG} = \frac{1}{4}\left( {\overrightarrow {OG} + \overrightarrow {OG} + \overrightarrow {OG} + \overrightarrow {OG} } \right) = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {AG} + \overrightarrow {OB} + \overrightarrow {BG} + \overrightarrow {OC} + \overrightarrow {CG} + \overrightarrow {OD} + \overrightarrow {DG} } \right)\]\[ = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\].
c) Đúng. \[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GA} + \overrightarrow {GC} + \overrightarrow {GD} = - \overrightarrow {GB} = \overrightarrow {BG} \].
d) Sai. \[\overrightarrow {AG} = \overrightarrow {AO} + \overrightarrow {OG} = \overrightarrow {AO} + \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right) = \overrightarrow {AO} + \frac{1}{4}\left( {4\overrightarrow {OA} + \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\]
\[ = \overrightarrow {AO} + \overrightarrow {OA} + \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right) = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.