Đẳng quá trình là quá trình biến đổi trạng thái của một khối khí xác định trong đó
Đẳng quá trình là quá trình biến đổi trạng thái của một khối khí xác định trong đó
A. một thông số không đổi, hai thông số thay đổi
B. hai thông số không đổi, một thông số thay đổi
C. ba thông số thay đổi
Quảng cáo
Trả lời:
Chọn A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
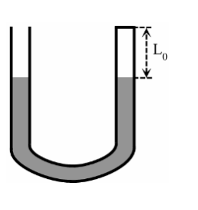
Áp suất tại 2 điểm màu xanh bằng nhau và đều bằng \({p_0}\) Thủy ngân bên nhánh phải dâng lên là \(30 - 25 = 5\;{\rm{cm}}\) Áp suất tại 2 điểm màu đỏ bằng nhau \( \Rightarrow p = {p_0} + h - 10\) Định luật Boyle \({p_0}{V_0} = pV \Rightarrow {p_0}S{L_0} = \left( {{p_0} + h - 10} \right)SL\)
\( \Rightarrow 75 \cdot 30 = (75 + h - 10) \cdot 25 \Rightarrow h = 25\;{\rm{cm}}\)
Trả lời ngắn: 25
Lời giải
\(\frac{{{p_1}{V_1}}}{{{T_1}}} = nR \Rightarrow \frac{{1,2 \cdot {{10}^5} \cdot 16 \cdot {{10}^{ - 3}}}}{{{T_1}}} = 8,31 \Rightarrow {T_1} \approx 231\;{\rm{K}} \Rightarrow \)a) Sai
\(p = aV + b \Rightarrow \left\{ {\begin{array}{*{20}{l}}{1,2 \cdot {{10}^5} = a \cdot 16 + b}\\{3 \cdot {{10}^5} = a \cdot 8 + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 22500}\\{b = 480000}\end{array}} \right.} \right.\)
\( \to p = - 22500 \cdot 12 + 480000 = 2,1 \cdot {10^5}\;{\rm{Pa}} \Rightarrow \)b) Đúng
\({T_{\max }}{\rm{ khi }}pV = - 22500{V^2} + 480000\) đạt max
\({(pV)^\prime } = 0 \Rightarrow - 22500 \cdot 2\;{\rm{V}} + 480000 = 0 \Rightarrow V = \frac{{32}}{3}{\rm{d}}{{\rm{m}}^3} \Rightarrow p = 2,4 \cdot {10^5}\;{\rm{Pa}}\)
\(\frac{{{{(pV)}_{\max }}}}{{{T_{\max }}}} = nR \Rightarrow \frac{{2,4 \cdot {{10}^5} \cdot \frac{{32}}{3} \cdot {{10}^{ - 3}}}}{{{T_{\max }}}} = 8,31 \Rightarrow {T_{\max }} \approx 308\;{\rm{K}} > 307\;{\rm{K}} \Rightarrow \)c) Đúng
\(\Delta U = \frac{3}{2}nR\left( {{T_2} - {T_1}} \right) = \frac{3}{2}\left( {{p_2}{V_2} - {p_1}{V_1}} \right) = \frac{3}{2} \cdot \left( {3 \cdot {{10}^5} \cdot 8 \cdot {{10}^{ - 3}} - 1,2 \cdot {{10}^5} \cdot 16 \cdot {{10}^{ - 3}}} \right) = 720\;{\rm{J}} \Rightarrow \)d) Đúng
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.