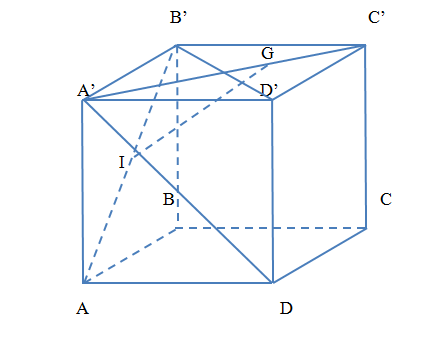
Cho hình hộp \[ABCD.{A_1}{B_1}{C_1}{D_1}\]. Chọn đẳng thức sai?
Cho hình hộp \[ABCD.{A_1}{B_1}{C_1}{D_1}\]. Chọn đẳng thức sai?
Câu hỏi trong đề: Đề kiểm tra Vectơ trong không gian (có lời giải) !!
Quảng cáo
Trả lời:
![Cho hình hộp \[ABCD.{A_1}{B_1}{C_1}{D_1}\]. Chọn đẳng thức sai? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/18-1759237938.png)
Ta có : \(\overrightarrow {BA} + \overrightarrow {D{D_1}} + \overrightarrow {B{D_1}} = \overrightarrow {BA} + \overrightarrow {B{B_1}} + \overrightarrow {B{D_1}} = \overrightarrow {B{A_1}} + \overrightarrow {B{D_1}} \ne \overrightarrow {BC} \) nên D sai.
Do \(\overrightarrow {BC} = \overrightarrow {{B_1}{C_1}} \)và \(\overrightarrow {BA} = \overrightarrow {{B_1}{A_1}} \) nên \(\overrightarrow {BC} + \overrightarrow {BA} = \overrightarrow {{B_1}{C_1}} + \overrightarrow {{B_1}{A_1}} \), nên A đúng
Do \(\overrightarrow {AD} + \overrightarrow {{D_1}{C_1}} + \overrightarrow {{D_1}{A_1}} = \overrightarrow {AD} + \overrightarrow {{D_1}{B_1}} = \overrightarrow {{A_1}{D_1}} + \overrightarrow {{D_1}{B_1}} = \overrightarrow {{A_1}{B_1}} = \overrightarrow {DC} \) nên
\(\overrightarrow {AD} + \overrightarrow {{D_1}{C_1}} + \overrightarrow {{D_1}{A_1}} = \overrightarrow {DC} \) nên B đúng.
Do \[\overrightarrow {BC} + \overrightarrow {BA} + \overrightarrow {B{B_1}} = \overrightarrow {BD} + \overrightarrow {D{D_1}} = \overrightarrow {B{D_1}} \] nên C đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số: \(3,08\)
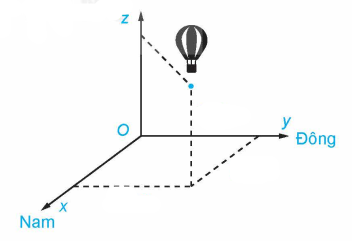
Với hệ trục toạ độ đã chọn thì vị trí hiện tại của khinh khí cầu là \(A\left( {2,5;1,7;0,6} \right)\).
Khi đó khoảng cách từ địa điểm xuất phát đến địa điểm hiện tại của khinh khí cầu là: \(OA = \sqrt {2,{5^2} + 1,{7^2} + 0,{6^2}} \approx 3,08\left( {km} \right)\)
Câu 2
Lời giải
Với \(k = 1\) ta có: \[\overrightarrow {AC} + \overrightarrow {BA'} + 1.\left( {\overrightarrow {DB} + \overrightarrow {C'D} } \right) = \overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {C'B} = \overrightarrow {AC} + \overrightarrow {C'A'} = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(k = \frac{1}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.