Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm \[O\] trên trần nhà lần lượt buộc vào ba điểm \[A,B,C\] trên đèn tròn sao cho tam giác \[ABC\] đều. Độ dài của ba đoạn dây \[OA,OB,OC\] đều bằng \[L\]. Trọng lượng của chiếc đèn là \[27N\] và bán kính của chiếc đèn là \(0,5m\).

Tìm chiều dài tối thiểu của mỗi sợi dây, biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là \(12N\). (Chiều dài tính theo đơn vị cm và làm tròn đến 1 số sau phần thập phân)
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm \[O\] trên trần nhà lần lượt buộc vào ba điểm \[A,B,C\] trên đèn tròn sao cho tam giác \[ABC\] đều. Độ dài của ba đoạn dây \[OA,OB,OC\] đều bằng \[L\]. Trọng lượng của chiếc đèn là \[27N\] và bán kính của chiếc đèn là \(0,5m\).

Tìm chiều dài tối thiểu của mỗi sợi dây, biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là \(12N\). (Chiều dài tính theo đơn vị cm và làm tròn đến 1 số sau phần thập phân)
Câu hỏi trong đề: Đề kiểm tra Vectơ trong không gian (có lời giải) !!
Quảng cáo
Trả lời:
Đáp số: \(75,6\)
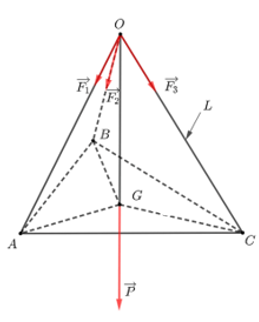
Gọi \[G\] là trọng tâm tam giác \[ABC\].
Vì tam giác \[ABC\] đều nên \[G\] là tâm đường tròn ngoại tiếp tam giác \[ABC\].
Do đó, \[GA = GB = GC = \]\(0,5m\).
Gọi \[F\] là độ lớn của các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) trên mỗi sợi dây. Khi đó, \(F = F\left( L \right)\) là một hàm số với biến số là \(L\).
Theo bài ra ta có \[OA = OB = OC = L\] nên \[OG \bot \left( {ABC} \right)\] và \[\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} } \right| = L\]
Do đó, \[\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\]
Vì vậy, tồn tại hằng số \[c \ne 0\] sao cho: \(\overrightarrow {{F_1}} = c\overrightarrow {OA} \), \(\overrightarrow {{F_2}} = c\overrightarrow {OB} ,\,\,\,\overrightarrow {{F_3}} = c\overrightarrow {OC} \). Suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = c\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\).
Theo quy tắc ba điểm ta có: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \).
Do đó: \[\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = 3c\overrightarrow {OG} \].
Mặt khác ta lại có \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \), với \(\overrightarrow P \) là trọng lực tác dụng lên chiếc đèn.
Mà trọng lượng tác dụng lên chiếc đèn là 20N nên \(\left| {\overrightarrow P } \right| = 27\)\( \Leftrightarrow 3c\left| {\overrightarrow {OG} } \right| = 27N \Leftrightarrow c = \frac{9}{{OG}}\) .
Tam giác \[OAG\] vuông tại \[G\](do \[OG \bot \left( {ABC} \right)\]) nên ta suy ra \(OG = \sqrt {O{A^2} - G{A^2}} = \sqrt {{L^2} - 0,{5^2}} \left( m \right)\) với \(L > 0,5\).
Do đó \(\left| {\overrightarrow {OG} } \right| = \sqrt {{L^2} - 0,{5^2}} \Rightarrow c = \frac{9}{{\sqrt {{L^2} - 0,{5^2}} }}\).
Khi đó \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {{F_1}} } \right| = c\left| {\overrightarrow {OA} } \right| = \frac{{9L}}{{\sqrt {{L^2} - 0,{5^2}} }}\) (với \(L > 0,5\))
Ta có lực căng tối đa của mỗi sợi dây là 12 N \( \Rightarrow F\left( L \right) \le 12 \Leftrightarrow \frac{{9L}}{{\sqrt {{L^2} - 0,{5^2}} }} \le 12 \Leftrightarrow 3L \le 4\sqrt {{L^2} - 0,{5^2}} \)\( \Leftrightarrow 9{L^2} \le 16{L^2} - 4 \Leftrightarrow 7{L^2} \ge 4 \Rightarrow L \ge \frac{2}{{\sqrt 7 }} \approx 0,756\) (m).
Vậy chiều dài tối thiểu của mỗi sợi dây là \(L = 0,756m = 75,6cm\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số: \(3,08\)
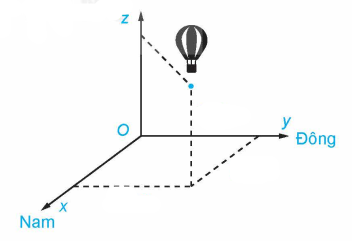
Với hệ trục toạ độ đã chọn thì vị trí hiện tại của khinh khí cầu là \(A\left( {2,5;1,7;0,6} \right)\).
Khi đó khoảng cách từ địa điểm xuất phát đến địa điểm hiện tại của khinh khí cầu là: \(OA = \sqrt {2,{5^2} + 1,{7^2} + 0,{6^2}} \approx 3,08\left( {km} \right)\)
Câu 2
Lời giải
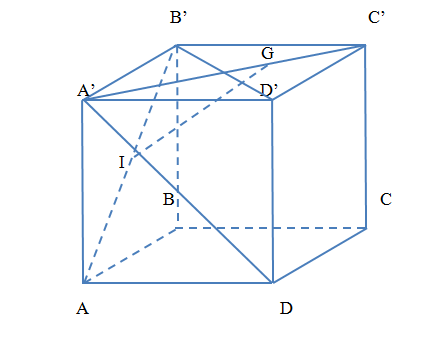
Với \(k = 1\) ta có: \[\overrightarrow {AC} + \overrightarrow {BA'} + 1.\left( {\overrightarrow {DB} + \overrightarrow {C'D} } \right) = \overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {C'B} = \overrightarrow {AC} + \overrightarrow {C'A'} = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(k = \frac{1}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.