Một đồ chơi có dạng hình tứ diện đều làm bằng thủy tinh có cạnh bằng \(10cm\). Bên trong đặt một đèn nhỏ. Đèn đặt trên đường nối từ đỉnh của tứ diện xuống tâm của đường tròn ngoại tiếp đa giác đáy và cách đỉnh một khoảng là \(\frac{{5\sqrt 6 }}{2}cm\). Đèn được nối bởi hai dây qua hai đỉnh của tứ diện như hình vẽ. Cường độ lực tổng hợp của hai dây tác dụng lên đèn là bao nhiêu?
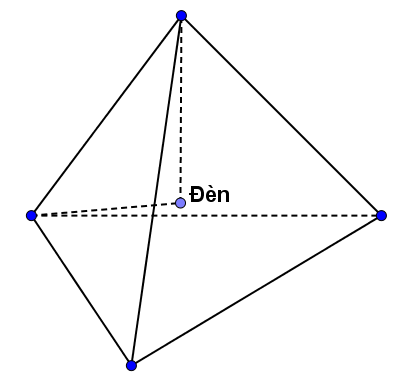
Một đồ chơi có dạng hình tứ diện đều làm bằng thủy tinh có cạnh bằng \(10cm\). Bên trong đặt một đèn nhỏ. Đèn đặt trên đường nối từ đỉnh của tứ diện xuống tâm của đường tròn ngoại tiếp đa giác đáy và cách đỉnh một khoảng là \(\frac{{5\sqrt 6 }}{2}cm\). Đèn được nối bởi hai dây qua hai đỉnh của tứ diện như hình vẽ. Cường độ lực tổng hợp của hai dây tác dụng lên đèn là bao nhiêu?

Quảng cáo
Trả lời:
Đáp án: \(\left| {\overrightarrow F } \right| = 5\sqrt 2 \) .
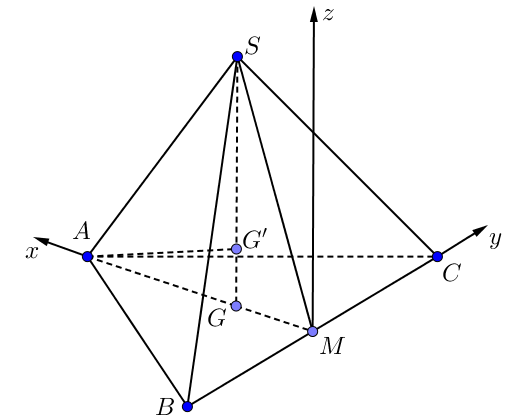
Gọi tứ diện là \(S.ABC\) và \(M,\,G,\,G'\) lần lượt là trung điểm của \(BC\), trọng tâm của \(\Delta ABC\)và vị trí đặt đèn.
\(S.ABC\) là tứ diện đều \( \Rightarrow \Delta ABC\) đều nên \(G\)là tâm của đường tròn ngoại tiếp \(\Delta ABC\).
\( \Rightarrow S,\,G',\,G\) thẳng hàng và \(SG' = \frac{{5\sqrt 6 }}{2}\).
Chọn hệ trục tọa độ \(Oxyz\) như hình vẽ sao cho \(M\left( {0;0;0} \right)\)
Có: \(AM = 5\sqrt 3 \), \(MG = \frac{1}{3}AM = \frac{{5\sqrt 3 }}{3}\),
\(AG = \frac{2}{3}AM = \frac{{10\sqrt 3 }}{3}\), \(SG = \sqrt {S{A^2} - A{G^2}} = \frac{{10\sqrt 6 }}{3}\) .
Khi đó: \(S\left( {\frac{{5\sqrt 3 }}{3};0;\frac{{10\sqrt 6 }}{3}} \right)\), \(A\left( {5\sqrt 3 ;0;0} \right)\), \(B\left( {0; - 5;0} \right)\), \(C\left( {0;5;0} \right)\)
\(G\) là trọng tâm của \(\Delta ABC\) \( \Rightarrow G\left( {\frac{{5\sqrt 3 }}{3};0;0} \right)\)\(\)
\( \Rightarrow SG' = \frac{3}{4}SG\) \( \Rightarrow \overrightarrow {SG'} = \frac{3}{4}\overrightarrow {SG} \)
\( \Rightarrow \left\{ \begin{array}{l}{x_{G'}} - {x_S} = \frac{3}{4}\left( {{x_G} - {x_S}} \right)\\{y_{G'}} - {y_S} = \frac{3}{4}\left( {{y_G} - {y_S}} \right)\\{z_{G'}} - {z_S} = \frac{3}{4}\left( {{z_G} - {z_S}} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_{G'}} = \frac{{5\sqrt 3 }}{3}\\{y_{G'}} = 0\\{x_{G'}} = \frac{{5\sqrt 6 }}{6}\end{array} \right.\) \( \Rightarrow G'\left( {\frac{{5\sqrt 3 }}{3};0;\frac{{5\sqrt 6 }}{6}} \right)\).
\( \Rightarrow G'A = \frac{{5\sqrt 6 }}{2}\).
\(\cos \left( {\overrightarrow {AG'} ,\overrightarrow {SG'} } \right) = \frac{{\overrightarrow {SG'} .\overrightarrow {AG'} }}{{\left| {\overrightarrow {SG'} } \right|.\left| {\overrightarrow {AG'} } \right|}} = - \frac{1}{3}\).
Gọi \(\overrightarrow F ,\,\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) lần lượt là lực tổng hợp và lực của hai dây tác dụng lên đèn
Có \(\overrightarrow F = \overrightarrow {F{}_1} + \overrightarrow {{F_2}} = \overrightarrow {AG'} + \overrightarrow {SG'} \)
\( \Rightarrow \left| {\overrightarrow F } \right| = \sqrt {{{\left( {\overrightarrow {AG'} + \overrightarrow {SG'} } \right)}^2}} \)
\( \Rightarrow \left| {\overrightarrow F } \right| = \sqrt {SG{'^2} + AG{'^2} + 2\overrightarrow {AG'} .\overrightarrow {SG'} } \)
\( \Rightarrow \left| {\overrightarrow F } \right| = \sqrt {SG{'^2} + AG{'^2} + 2AG'.SG'.\cos \left( {\overrightarrow {AG'} ,\overrightarrow {SG'} } \right)} \)
\( \Rightarrow \left| {\overrightarrow F } \right| = \sqrt {{{\left( {\frac{{5\sqrt 6 }}{2}} \right)}^2} + {{\left( {\frac{{5\sqrt 6 }}{2}} \right)}^2} + 2.\frac{{5\sqrt 6 }}{2}.\frac{{5\sqrt 6 }}{2}.\left( { - \frac{1}{3}} \right)} \) \( = 5\sqrt 2 \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
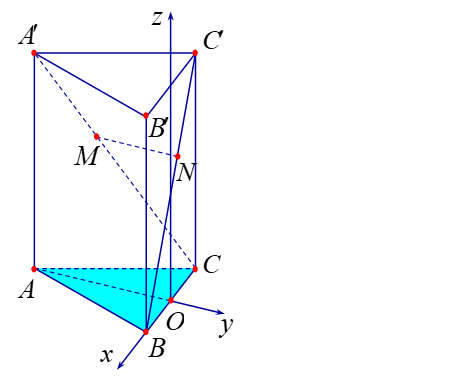
Chọn hệ trục tọa độ \[Oxyz\] như hình vẽ (\(O\) là trung điểm của \(BC\)). Ta có: \(A'\left( {0;\, - 150\sqrt 3 ;\,300} \right),\) \(B\left( {150;\,0;\,0} \right),\) \(C\left( { - 150;\,0;\,0} \right),\) \(C'\left( { - 150;\,0;\,300} \right),\)\(\overrightarrow {CA'} = \left( {150;\, - 150\sqrt 3 ;\,300} \right)\), \(\overrightarrow {BC'} = \left( { - 300;\,0;\,300} \right)\)
Gọi \(m,n\) thỏa mãn \(\left\{ \begin{array}{l}\overrightarrow {CM} = m\overrightarrow {CA'} \\\overrightarrow {BN} = n\overrightarrow {BC'} \end{array} \right.\) ta có \(M\left( { - 150 + 150m;\, - 150\sqrt 3 m;\,300m} \right)\), \(N\left( {150 - 300n;\,0;\,300n} \right)\)
\( \Rightarrow \overrightarrow {MN} = \left( { - 150m - 300n + 300;\,150\sqrt 3 m;\,300n - 300m} \right)\).
Đường thẳng \(MN\) là đường vuông góc chung của \(A'C\) và \(BC'\)nên:
\(\left\{ \begin{array}{l}\overrightarrow {MN} .\overrightarrow {CA'} = 0\\\overrightarrow {MN} .\overrightarrow {BC'} = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l} - 4m + n = - 1\\ - m + 4n = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m = \frac{2}{5}\\n = \frac{3}{5}\end{array} \right.\)\( \Rightarrow \overrightarrow {MN} = \left( {60;\,60\sqrt 3 ;\,60} \right) \Rightarrow MN = 60\sqrt 5 \)
Số tiền xây cầu là: \(T = 60\sqrt 5 .5 \approx 671\)tỷ đồng.
Lời giải
|
a) Đúng |
b) Đúng |
c) Sai |
d) Sai |
a) Đúng
Ta có: \(\overrightarrow {AB} = \left( { - 2;1;2} \right),\,\overrightarrow {AC} = \left( { - 2; - 4;4} \right)\)
\( \Rightarrow \cos A = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \frac{4}{9} > 0 \Rightarrow A\) là góc nhọn.
b) Đúng
\(D\) đối xứng với \(A\) qua \(B\) nên \(B\) là trung điểm của \(AD\)
\( \Rightarrow \left\{ \begin{array}{l}{x_B} = \frac{{{x_A} + {x_D}}}{2}\\{y_B} = \frac{{{y_A} + {y_D}}}{2}\\{z_B} = \frac{{{z_A} + {z_D}}}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_D} = 2{x_B} - {x_A}\\{y_D} = 2{y_B} - {y_A}\\{z_D} = 2{z_B} - {z_A}\end{array} \right. \Rightarrow D\left( { - 6;2;1} \right)\)
c) Sai
Ta có: \[AB = 3;AC = 6\]\[ \Rightarrow \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{1}{2} \Rightarrow \overrightarrow {DC} = - 2\overrightarrow {DB} \]
\[ \Rightarrow \left\{ \begin{array}{l}{x_C} - {x_D} = - 2\left( {{x_B} - {x_D}} \right)\\{y_C} - {y_D} = - 2\left( {{y_B} - {y_D}} \right)\\{z_C} - {z_D} = - 2\left( {{z_B} - {z_D}} \right)\end{array} \right. \Rightarrow D\left( { - 4; - \frac{2}{3}; - \frac{1}{3}} \right) \Rightarrow AD = \frac{{2\sqrt {26} }}{3}\].
d) Sai
![Trong không gian \(Oxyz\), cho tam giác \(ABC\) có \[A\left( { - 2;0; - 3} \right),B\left( { - 4;1; - 1} \right),C\left( { - 4; - 4;1} \right)\]. a) Góc \(A\) là góc nhọn. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/7-1759365178.png)
Vì \(M \in \left( {Oyz} \right) \Rightarrow a = 0 \Rightarrow M\left( {0;b;c} \right)\)
Ta có: \(A,\,B\) nằm cùng phía đối với \(\left( {Oyz} \right)\).
Gọi \(A'\) là điểm đối xứng với \(A\) qua \(\left( {Oyz} \right) \Rightarrow A'\left( {2;0; - 3} \right)\)
Khi đó: \(MA + MB = MA' + MB \ge A'B\)
Do đó: \(MA + MB\) đạt GTNN khi \(A',M,B\) thẳng hàng.
\(\overrightarrow {A'B} = \left( { - 6;1;2} \right),\,\overrightarrow {A'M} = \left( { - 2;b;c + 3} \right)\)
\(A',\,B,\,M\) thẳng hàng \( \Leftrightarrow \overrightarrow {A'B} ,\,\overrightarrow {A'M} \) cùng phương\( \Leftrightarrow \frac{{ - 2}}{{ - 6}} = \frac{b}{1} = \frac{{c + 3}}{2} \Rightarrow \left\{ \begin{array}{l}b = \frac{1}{3}\\c = - \frac{7}{3}\end{array} \right.\)
Vậy \(M\left( {0;\frac{1}{3}; - \frac{7}{3}} \right) \Rightarrow a + b + c = - 2\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
PHẦN II. TRẮC NGHIỆM ĐÚNG SAI
Trong không gian với hệ trục tọa độ Oxyz, cho \(A\left( {1; - 1;2} \right)\), \(B\left( { - 2;0;3} \right)\), \(C\left( {0;1; - 2} \right)\). Các mệnh đề sau đúng hay sai?
a) Tọa độ trọng tâm tam giác \(ABC\) là \(G\left( {\frac{{ - 1}}{3};0;1} \right)\).
b) Độ dài đoạn thẳng \(AB = \sqrt {11} \).
c) Tích có hướng \([\overrightarrow {AB} ,\,\overrightarrow {AC} ] = \left( { - 6;13; - 5} \right)\).
d) \(M\left( {a;b;c} \right)\)là điểm thuộc mặt phẳng \[\left( {Oxy} \right)\] sao cho biểu thức \[S = 2.\overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MB} .\overrightarrow {MC} + \overrightarrow {MC} .\overrightarrow {MA} \] đạt giá trị nhỏ nhất. Khi đó biểu thức \[T = a - b + c = \frac{1}{4}\].
Trong không gian với hệ trục tọa độ Oxyz, cho \(A\left( {1; - 1;2} \right)\), \(B\left( { - 2;0;3} \right)\), \(C\left( {0;1; - 2} \right)\). Các mệnh đề sau đúng hay sai?
a) Tọa độ trọng tâm tam giác \(ABC\) là \(G\left( {\frac{{ - 1}}{3};0;1} \right)\).
b) Độ dài đoạn thẳng \(AB = \sqrt {11} \).
c) Tích có hướng \([\overrightarrow {AB} ,\,\overrightarrow {AC} ] = \left( { - 6;13; - 5} \right)\).
d) \(M\left( {a;b;c} \right)\)là điểm thuộc mặt phẳng \[\left( {Oxy} \right)\] sao cho biểu thức \[S = 2.\overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MB} .\overrightarrow {MC} + \overrightarrow {MC} .\overrightarrow {MA} \] đạt giá trị nhỏ nhất. Khi đó biểu thức \[T = a - b + c = \frac{1}{4}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.