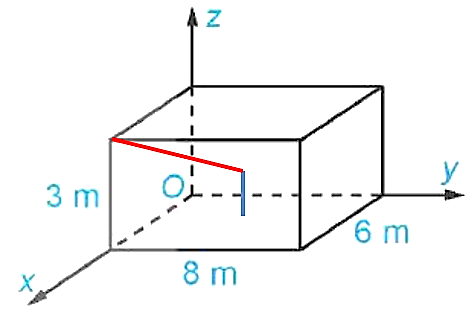
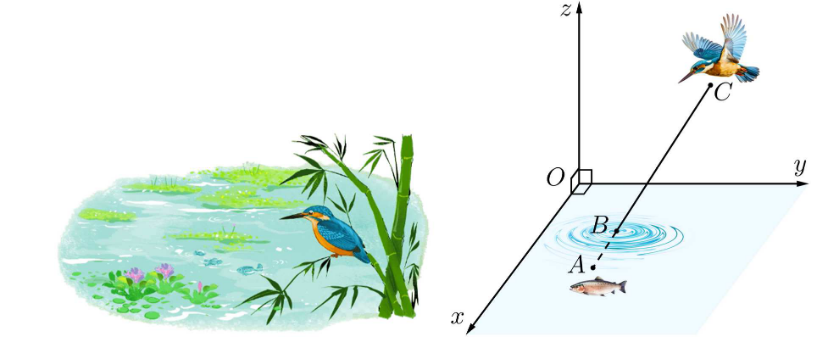
Trong không gian \[{\rm{O}}xyz\] cho hai vec tơ \[\overrightarrow a = (1; - 2;0),\,\,\overrightarrow b = (1;3; - 2)\]. Góc giữa hai vec tơ \[\overrightarrow a \] và \[\,\,\overrightarrow b \] bằng bao nhiêu ( tính theo độ làm tròn đến hàng phần chục)
Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
\[cos\left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{1 - 6}}{{\sqrt {{1^2} + {{( - 2)}^2} + 0} .\sqrt {{1^2} + {3^2} + {{( - 2)}^2}} }} = \frac{{ - 5}}{{\sqrt 5 .\sqrt {14} }}\]
Vậy \[\left( {\overrightarrow a ,\overrightarrow b } \right) \approx 126,7\]
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hệ tọa độ \[{\rm{O}}xyz\] như hình vẽ, ta có vị trí mạng nhện ở \[A(6;0;3)\] vị trí cầm chổi \[B(3;4;\frac{3}{2})\], Vậy chổi phải có độ dài \[AB = \sqrt {{{(3 - 6)}^2} + {{(4 - 0)}^2} + {{(\frac{3}{2} - 3)}^2}} = \frac{{\sqrt {109} }}{2} \approx 5.22(m)\]
Lời giải
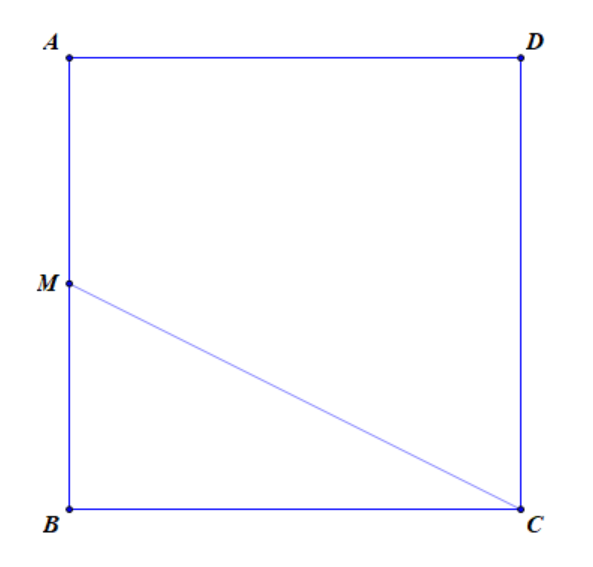
\(\overrightarrow {BD} = \left( { - 8; - 4; - 8} \right)\)\( \Rightarrow BD = 12\)\( \Rightarrow AB = \frac{{12}}{{\sqrt 2 }}\)\( = 6\sqrt 2 \).
Gọi \(M\)là trung điểm \(AB\)\( \Rightarrow MC = 3\sqrt {10} \).
\(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right|\)\( = \left| {2\overrightarrow {CM} } \right|\)\( = 2CM\)\( = 6\sqrt {10} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Vec tơ cùng vuông góc với vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) có tọa độ bằng \(\left( { - 5; - 7; - 3} \right)\).
B. Vectơ \(\overrightarrow a \) không cùng phương với vectơ \(\overrightarrow b \).
C. Vectơ \(\overrightarrow a \) không vuông góc với vectơ \(\overrightarrow b \).
D. \(\left| {\overrightarrow a } \right| = 14\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\overrightarrow {AB} .\overrightarrow {CD} = - 4\).
B. \(\overrightarrow {AB} .\overrightarrow {CD} = 2\).
C. \(\overrightarrow {AB} .\overrightarrow {CD} = 1\).
D. \(\overrightarrow {AB} .\overrightarrow {CD} = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập