khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 12
  3. Toán

Câu hỏi:

02/10/2025 10,271 Lưu

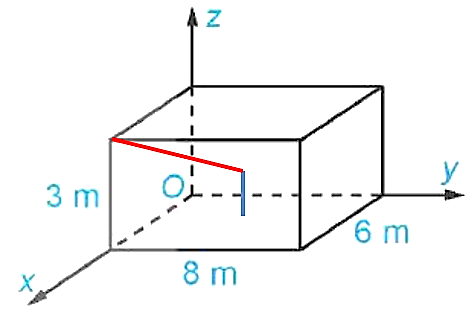
Trong một phòng học được thiết kế dạng hình hộp chữ nhật, với chiều dài \[8m\], chiều rộng \[6m\] và chiều cao \[3m\]. Hai bạn An và Bình làm nhiệm vụ trực nhật, mạng nhện cần quét ở góc ngoài cùng trên trần nhà, An bảo không nên đứng ngay vị trí đó ở nền nhà quét vì sẽ bụi rơi xuông người mình, An lại đố bạn Bình ‘nếu mình đứng ở giữa nhà quét thì mình phải kéo chối quét nhà dài ra mấy mét ( làm tròn đến hàng phần trăm) để quét được vị trí mạng nhên, biết An cầm chổi cao \[1,5m\]’. Bình trả lời đứng vị trí đó chổi dài \[5m\] cũng không tới. Hỏi Bình đã tính được bao nhiêu?
Trong một phòng học được thiết kế dạng hình hộp chữ nhật, với chiều dài 8m, chiều rộng 6m và chiều cao 3m. Hai bạn An và Bình làm nhiệm vụ trực nhật, mạng nhện cần quét ở góc ngoài cùng trên trần nhà, (ảnh 1)

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra Bài tập cuối chương 2 lớp 12 (có lời giải) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack
Xét hệ tọa độ \[{\rm{O}}xyz\] như hình vẽ, ta có vị trí mạng nhện ở \[A(6;0;3)\] vị trí cầm chổi \[B(3;4;\frac{3}{2})\], Vậy chổi phải có độ dài \[AB = \sqrt {{{(3 - 6)}^2} + {{(4 - 0)}^2} + {{(\frac{3}{2} - 3)}^2}}  = \frac{{\sqrt {109} }}{2} \approx 5.22(m)\]

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD,  B3;0;8,  D−5;−4;0. Biết đỉnh \(A\) thuộc mặt phẳng \(\left( {Oxy} \right)\) và có tọa độ là những số nguyên, khi đó \(\left| {\overrightarrow {CA}  + \overrightarrow {CB} } \right|\) bằng:

Lời giải

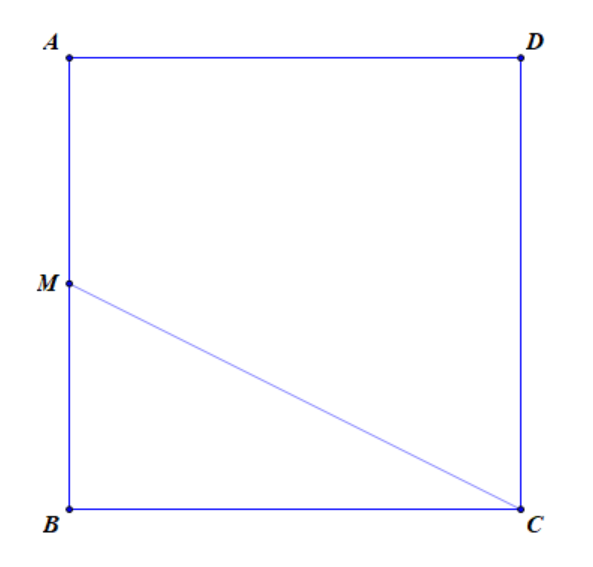
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD,\,\,B\left( {3;0;8} \right),\,\,D\left( { - 5; - 4;0} \right)\). Biết đỉnh \(A\) thuộc mặt phẳ (ảnh 1)

\(\overrightarrow {BD}  = \left( { - 8; - 4; - 8} \right)\)\( \Rightarrow BD = 12\)\( \Rightarrow AB = \frac{{12}}{{\sqrt 2 }}\)\( = 6\sqrt 2 \).

Gọi \(M\)là trung điểm \(AB\)\( \Rightarrow MC = 3\sqrt {10} \).

\(\left| {\overrightarrow {CA}  + \overrightarrow {CB} } \right|\)\( = \left| {2\overrightarrow {CM} } \right|\)\( = 2CM\)\( = 6\sqrt {10} \).

Câu 2

 Với hệ trục tọa độ Oxyz sao cho O nằm trên mặt nước, mặt phẳng \(\left( {Oxy} \right)\)là mặt nước, trục \(Oz\) hướng lên trên (đơn vị đo: mét), một con chim bói cá đang ở vị trí cách mặt nước \(2m\), cách mặt phẳng \(\left( {Oxz} \right),\,\left( {Oyz} \right)\) lần lượt là \(3m\) và \(1m\) phóng thẳng xuống vị trí con cá, biết con cá cách mặt nước \(50\,cm\), cách mặt phẳng \(\left( {Oxz} \right),\,\left( {Oyz} \right)\) lần lượt là \(1m\) và \(1,5\,m\)Tìm tọa độ điểm \(B\) lúc chim bói cá vừa tiếp xúc với mặt nước.
 Với hệ trục tọa độ Oxyz sao cho O nằm trên mặt nước, mặt phẳng \(\left( {Oxy} \right)\)là mặt nước, trục \(Oz\) h (ảnh 1)

Lời giải

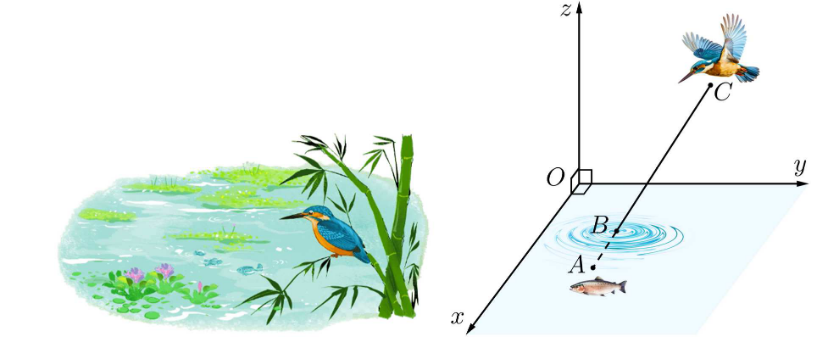
Ta có: \(A\left( {1,5;1; - 0,5} \right)\) và \(C\left( {1;3;2} \right)\)

\(\overrightarrow {AC} \left( { - 0,5;2;2,5} \right)\)

Khi đó phương trình đường thẳng \(AC\) là\(\left\{ \begin{array}{l}x =  - 0,5t + 1\\y = 2t + 3\\z = 2,5t + 2\end{array} \right.\) suy ra \(2,5t + 2 = 0 \Rightarrow t =  - \frac{4}{5}\).

Khi đó \(\left\{ \begin{array}{l}x = \frac{7}{5}\\y = \frac{7}{5}\\z = 0\end{array} \right.\) hay \(B\left( {\frac{7}{5};\frac{7}{5};0} \right)\)

Câu 3

 Cho tứ diện đều ABCD có cạnh bằng \(2\). Tính \(\overrightarrow {AB} .\overrightarrow {CD} \).
A. \(\overrightarrow {AB} .\overrightarrow {CD} = - 4\).                              
B. \(\overrightarrow {AB} .\overrightarrow {CD} = 2\).                         
C. \(\overrightarrow {AB} .\overrightarrow {CD} = 1\).                              
D. \(\overrightarrow {AB} .\overrightarrow {CD} = 0\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

 Trong không gian với hệ trục tọa độ Oxyz cho \(\overrightarrow a = \left( {1; - 2;3} \right)\) và \(\overrightarrow b = \left( {2; - 1; - 1} \right)\).Cho các mệnh đề sau. Mệnh đề nào là mệnh đề SAI?
A. Vec tơ cùng vuông góc với vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) có tọa độ bằng \(\left( { - 5; - 7; - 3} \right)\).
B. Vectơ \(\overrightarrow a \) không cùng phương với vectơ \(\overrightarrow b \).
C. Vectơ \(\overrightarrow a \) không vuông góc với vectơ \(\overrightarrow b \).
D. \(\left| {\overrightarrow a } \right| = 14\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một căn phòng dạng hình hộp chữ nhật với chiều dài \(8m\), rộng\(6m\)và cao\(4m\) có hai chiếc quạt treo tường. Chiếc quạt A treo chính giữa bức tường \(8m\)và cách trần\(1m\), chiếc quạt B treo chính giữa bức tường \(6m\)và cách trần \(1,5m\). Hỏi khoảng cách giữa hai chiếc quạt AB cách nhau bao nhiêu m ( làm tròn đến hàng phần nghìn)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình hộp ABCD.A'B'C'D'; Các điểm \(M,\,N\)lần lượt thuộc các đường thẳng CA và \(DC'\)sao cho \(\overrightarrow {MC}  = m\overrightarrow {MA} ;\,\,\overrightarrow {ND}  = m\overrightarrow {NC'} \). Đặt \[\overrightarrow {BA}  = \overrightarrow a \,;\,\,\overrightarrow {BB'}  = \overrightarrow b ;\,\overrightarrow {BC}  = \overrightarrow c \]

a)\(\overrightarrow {BD'}  = \overrightarrow a  + \overrightarrow b  - \overrightarrow c \).

b)\(\overrightarrow {BM}  = \frac{{\overrightarrow c  - m\overrightarrow a }}{{1 - m}}\).

c) \(\overrightarrow {BN}  = \frac{1}{{1 - m}}\overrightarrow a  - \frac{m}{{1 - m}}\overrightarrow b  + \overrightarrow c \).

d) \(m = \frac{1}{2}\) thì \(MN\)//\(BD'\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập