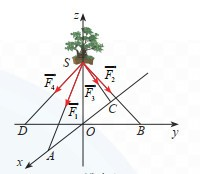
(1,0 điểm) Một chậu cây được đặt trên một giá đỡ có bốn chân với điểm đặt \(S\left( {0;0;30} \right)\) và các điểm chạm mặt đất của bốn chân lần lượt là \(A\left( {30;0;0} \right),B\left( {0;20;0} \right),C\left( { - 20;0;0} \right),D\left( {0; - 20;0} \right)\) (đơn vị cm). Cho biết trọng lực tác dụng lên chậu cây có độ lớn \(60N\)và được phân bố thành bốn lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} ,\overrightarrow {{F_4}} \) có độ lớn bằng nhau như hình vẽ. Tính \(\left| {\overrightarrow {{F_1}} + 2\overrightarrow {{F_2}} + 3\overrightarrow {{F_3}} + 4\overrightarrow {{F_4}} } \right|\) (kết quả làm tròn đến hàng đơn vị)

Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!
Quảng cáo
Trả lời:
Tứ giác \(ABCD\) có hai đường chéo bằng nhau và vuông góc với nhau tại trung điểm của mỗi đường nên là hình vuông.
Ta có: \(\overrightarrow {SA} = \left( {30;0; - 30} \right),\overrightarrow {SB} = \left( {0;20; - 20} \right),\overrightarrow {SC} = \left( { - 20;0; - 20} \right),\overrightarrow {SD} = \left( {0; - 20; - 20} \right)\)
\( \Rightarrow SA = SB = SC = SD = 30\sqrt 2 \). Do đó \(S.ABCD\) là hình chóp tứ giác đều.
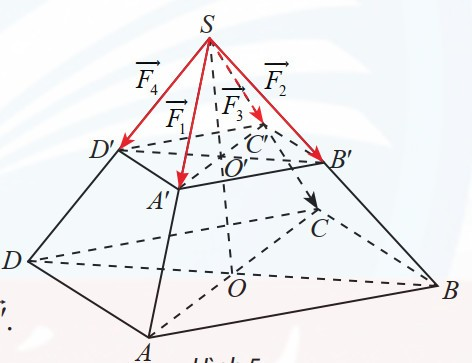
Các vecto \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} ,\overrightarrow {{F_4}} \) có điểm đầu tại \(S\) và điểm cuối lần lượt là \(A',B',C',D'\).
Ta có \(SA' = SB' = SC' = SD'\) nên \(S.A'B'C'D'\) cũng là hình chóp tứ giác đều.
Gọi \(\overrightarrow F \) là trọng lực tác dụng lên chậu cây và \(O'\) là tâm của hình vuông \(A'B'C'D'\). Ta có:
\[\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} = \overrightarrow {SA'} + \overrightarrow {SB'} + \overrightarrow {SC'} + \overrightarrow {SD'} = 4\overrightarrow {SO'} \]
Ta có: \(\left| {\overrightarrow F } \right| = 60 \Rightarrow \left| {\overrightarrow {SO'} } \right| = SO = 15\).
Do tam giác \(SO'A'\) vuông cân nên \(SA' = SO'\sqrt 2 = 15\sqrt 2 = \frac{1}{2}SA \Rightarrow \overrightarrow {{F_1}} = \overrightarrow {SA'} = \frac{1}{2}\overrightarrow {SA} = \left( {15;0; - 15} \right)\)
Chứng minh tương tự ta cũng có:
\(\overrightarrow {{F_2}} = \frac{1}{2}\overrightarrow {SB} = \left( {0;15; - 15} \right),\overrightarrow {{F_3}} = \frac{1}{2}\overrightarrow {SC} = \left( { - 15;0; - 15} \right),\overrightarrow {{F_4}} = \frac{1}{2}\overrightarrow {SD} = \left( {0; - 15; - 15} \right)\)
Suy ra: \(\overrightarrow {{F_1}} + 2\overrightarrow {{F_2}} + 3\overrightarrow {{F_3}} + 4\overrightarrow {{F_4}} = \left( { - 30; - 30; - 150} \right) \Rightarrow \left| {\overrightarrow {{F_1}} + 2\overrightarrow {{F_2}} + 3\overrightarrow {{F_3}} + 4\overrightarrow {{F_4}} } \right| = 90\sqrt 3 \approx 156\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số: \(10\sqrt 3 \,\,\left( N \right)\).
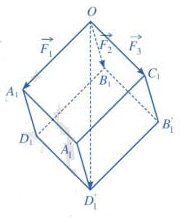
Gọi \({A_1},{B_1},{C_1}\) lần lượt là các điểm sao cho \(\overrightarrow {O{A_1}} = \overrightarrow {{F_1}} ,{\rm{ }}\overrightarrow {O{B_1}} = \overrightarrow {{F_2}} ,{\rm{ }}\overrightarrow {O{C_1}} = \overrightarrow {{F_3}} \)
Lấy các điểm sao cho là hình hộp.
Theo quy tắc hình hộp ta có:
Do các lực căng \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) đôi một vuông góc với nhau và có độ lớn: \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 10\left( N \right)\) nên hình hộp có ba cạnh \(OA,OB,OC\) đôi một vuông góc và bằng nhau. Vì thế là hình lập phương có độ dài cạnh bằng \(10\), suy ra độ dài đường chéo bằng \(10\sqrt 3 \)
Lời giải
![Cho tứ diện ABCD có AB = AC = AD = a \[\widehat {BAC} = \widehat {BAD} = 60^\circ ,\,\] \[\widehat {CAD} = 90^\circ \]. Gọi \(I\) là điểm trên c (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/8-1759379625.png)
Ta có: \(\overrightarrow {IJ} \,.\overrightarrow {AB} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AD} - \frac{3}{2}\overrightarrow {AB} } \right).\overrightarrow {AB} = \,\frac{1}{2}\left( {\overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {AD} .\overrightarrow {AB} - \frac{3}{2}{{\overrightarrow {AB} }^2}} \right)\)
Lại có \[\overrightarrow {AB} .\overrightarrow {AD} = AB.AD.cos60^\circ = \frac{{{a^2}}}{2}\]
\[\overrightarrow {AC} .\overrightarrow {AB} = \overrightarrow {AC} .\overrightarrow {AB} = AC.AB.cos60^\circ = \frac{{{a^2}}}{2}\].
Vậy: \(\overrightarrow {IJ} \,.\overrightarrow {AB} = \frac{1}{2}\left( {\frac{{{a^2}}}{2} + \frac{{{a^2}}}{2} - \frac{3}{2}{a^2}} \right) = - \frac{{{a^2}}}{4}\)
Có \[\widehat {CAD} = 90^\circ \Rightarrow \overrightarrow {AC} .\overrightarrow {AD} = 0.\]
\(\overrightarrow {IJ} \, = \,\overrightarrow {IA} + \overrightarrow {AJ} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AD} - \frac{3}{2}\overrightarrow {AB} } \right)\)
\(I{J^2} = {\overrightarrow {IJ} ^2}\, = \frac{1}{4}{\left( {\overrightarrow {AC} + \overrightarrow {AD} - \frac{3}{2}\overrightarrow {AB} } \right)^2} = \frac{1}{4}\left( {\frac{{17}}{4}{a^2} + 2\overrightarrow {AC} .\overrightarrow {AD} - 3\overrightarrow {AC} .\overrightarrow {AB} - 3\overrightarrow {AB} .\overrightarrow {AD} } \right) = \frac{{5{a^2}}}{{16}}\)
\( \Rightarrow IJ = \frac{{a\sqrt 5 }}{4}.\)
Vậy: \(\cos \left( {\overrightarrow {IJ} \,,\overrightarrow {AB} } \right) = \frac{{\overrightarrow {IJ} \,.\overrightarrow {AB} }}{{IJ.AB}} = \frac{{ - \frac{{{a^2}}}{4}}}{{\frac{{a\sqrt 5 }}{4}.a}} = - \frac{{\sqrt 5 }}{5}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.