Trong y học, như ở hình bên, người ta dùng từ trường tác động lên một số vùng trong não, tạo ra dòng điện để chữa trị các bệnh về thần kinh (TMS – Transcranial Magnetic Stimulation). Bằng phương pháp này, tại một vùng mô trong não có dạng hình tròn bán kính $r = 0{,}10\ \text{cm}$, người ta tạo ra một từ trường đều có hướng sức từ vuông góc với mặt phẳng chứa mô đó, có độ lớn biến thiên đều theo thời gian với lượng $\Delta B = 0{,}20\ \text{T}$ trong $\Delta t = 75\ \text{ms}$. Suất điện động cảm ứng xuất hiện trong vùng mô này bằng bao nhiêu $\mu\text{V}$ (làm tròn đến chữ số hàng phần mười)?
Trong y học, như ở hình bên, người ta dùng từ trường tác động lên một số vùng trong não, tạo ra dòng điện để chữa trị các bệnh về thần kinh (TMS – Transcranial Magnetic Stimulation). Bằng phương pháp này, tại một vùng mô trong não có dạng hình tròn bán kính $r = 0{,}10\ \text{cm}$, người ta tạo ra một từ trường đều có hướng sức từ vuông góc với mặt phẳng chứa mô đó, có độ lớn biến thiên đều theo thời gian với lượng $\Delta B = 0{,}20\ \text{T}$ trong $\Delta t = 75\ \text{ms}$. Suất điện động cảm ứng xuất hiện trong vùng mô này bằng bao nhiêu $\mu\text{V}$ (làm tròn đến chữ số hàng phần mười)?

Quảng cáo
Trả lời:
Suất điện động cảm ứng trong vùng mô hình tròn có độ lớn
\[
e=\left|\frac{\Delta\Phi}{\Delta t}\right|
=\left|\frac{\Delta(BS)}{\Delta t}\right|
= S\left|\frac{\Delta B}{\Delta t}\right|
= \pi r^{2}\,\frac{\Delta B}{\Delta t}.
\]
Đổi đơn vị: $r=0{,}10\ \text{cm}=1{,}0\times 10^{-3}\ \text{m}$, $\Delta t=75\ \text{ms}=75\times 10^{-3}\ \text{s}$. Thay số:
\[
e=\pi(1{,}0\times 10^{-3})^{2}\cdot \frac{0{,}20}{75\times 10^{-3}}
\approx 8{,}4\times 10^{-6}\ \text{V}
= 8{,}4\ \mu\text{V}.
\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Với quá trình làm nóng đẳng áp:
\[
U - U_0 = A_1 + Q_1,\qquad
A_1 = -\,p\,\Delta V = -\,\frac{m}{M}R\,\Delta T,\quad Q_1=12\ \text{J}.
\]
Với quá trình làm lạnh đẳng tích để trở về nhiệt độ ban đầu:
\[
U_0 - U = A_2 + Q_2,\qquad A_2=0,\ Q_2=-9\ \text{J}\ \Rightarrow\ U-U_0=9.
\]
Kết hợp hai biểu thức:
\[
-\frac{m}{M}R\,\Delta T + 12 = 9 \ \Rightarrow\ \frac{m}{M}R\,\Delta T = 3
\ \Rightarrow\ m=\frac{3M}{R\,\Delta T}.
\]
Thay số $M=28\ \text{g/mol}$, $R=8{,}31\ \text{J/(mol·K)}$, $\Delta T=15\ \text{K}$:
\[
m=\frac{3\cdot 28}{8{,}31\cdot 15}\ \text{g}\approx 0{,}67\ \text{g}.
\]
Lời giải
Đáp án đúng là B
Dùng phương trình Claperon $pV = \dfrac{m}{M}RT$ ta tìm được biểu thức tính khối lượng riêng của không khí là
\[
\rho = \dfrac{m}{V} = \dfrac{pM}{RT}.
\]
Áp dụng công thức trên ta tìm được khối lượng riêng của không khí trong đèn trời, ngoài đèn trời và không khí ở điều kiện tiêu chuẩn lần lượt là
\[
\rho_1 = \dfrac{pM}{RT_1},\qquad
\rho_2 = \dfrac{pM}{RT_2},\qquad
\rho_0 = \dfrac{p_0 M}{RT_0}.
\]
Để đèn trời bay lên được thì phải có $F_A \ge p_{\text{đèn}} + p_{\text{khi}}$ hay $\rho_2 g V \ge m g + \rho_1 g V$ dẫn đến
\[
m \le (\rho_2 - \rho_1)V
= \left(\dfrac{pM}{RT_2} - \dfrac{pM}{RT_1}\right)V
= \left(\dfrac{1}{T_2} - \dfrac{1}{T_1}\right)\dfrac{pMV}{R}.
\]
Từ $\rho_0 = \dfrac{p_0 M}{RT_0} \Rightarrow \dfrac{pM}{R} = \rho_0 T_0 \dfrac{p}{p_0}$ nên
\[
m \le \left(\dfrac{1}{T_2} - \dfrac{1}{T_1}\right) T_0 \dfrac{p}{p_0}\, \rho_0\, V.
\]
Thay số ta được
\[
m \le \left(\dfrac{1}{27+273} - \dfrac{1}{67+273}\right)\cdot 273 \cdot \dfrac{10^5}{1{,}013\cdot 10^5}\cdot 1{,}29 \cdot 0{,}10
\approx 13{,}6 \cdot 10^{-3}\ \text{kg} = 13{,}6\ \text{g}.
\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
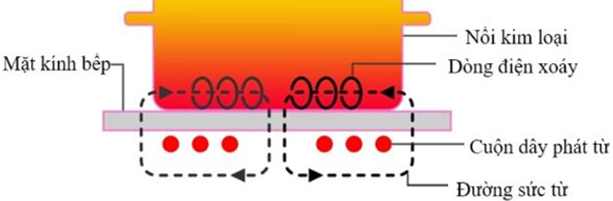
A. Bếp từ hoạt động dựa trên tác dụng phát quang của dòng điện.
B. Bếp từ có thể sử dụng trực tiếp dòng điện không đổi.
C. Nồi kim loại nóng lên là do tác dụng nhiệt của dòng điện cảm ứng sinh ra ở đáy nồi.
D. Nồi kim loại nóng lên là do nhiệt sinh ra từ mặt bếp từ truyền lên nồi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. nhận nhiệt.
B. sinh công.
C. tỏa nhiệt.
D. nhận công.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.