Thả đồng thời 0,6 kg sắt ở nhiệt độ 37 °C và 450 g đồng ở nhiệt độ 27 °C vào 1,5 kg nước ở nhiệt độ 57 °C. Biết nhiệt dung riêng của sắt, đồng và nước lần lượt là 460 J/(kg·K), 400 J/(kg·K) và 4200 J/(kg·K). Bỏ qua sự tỏa nhiệt ra môi trường và sự hóa hơi của nước. Nhiệt độ của hỗn hợp khi xảy ra sự cân bằng nhiệt bằng bao nhiêu °C? (Làm tròn kết quả đến chữ số hàng đơn vị)
Thả đồng thời 0,6 kg sắt ở nhiệt độ 37 °C và 450 g đồng ở nhiệt độ 27 °C vào 1,5 kg nước ở nhiệt độ 57 °C. Biết nhiệt dung riêng của sắt, đồng và nước lần lượt là 460 J/(kg·K), 400 J/(kg·K) và 4200 J/(kg·K). Bỏ qua sự tỏa nhiệt ra môi trường và sự hóa hơi của nước. Nhiệt độ của hỗn hợp khi xảy ra sự cân bằng nhiệt bằng bao nhiêu °C? (Làm tròn kết quả đến chữ số hàng đơn vị)
Quảng cáo
Trả lời:
Áp dụng phương trình cân bằng nhiệt, ta có:
\(|Q_{\text{toả}}| = |Q_{\text{thu}}| \Rightarrow m_g c_g (t_{\text{cb}}-37) + m_d c_d (t_{\text{cb}}-27) = m_n c_n (57 - t_{\text{cb}})\)
\(\Rightarrow 0{,}6\cdot 460\cdot (t_{\text{cb}}-37) + 450\cdot 10^{-3}\cdot 400\cdot (t_{\text{cb}}-27) = 1{,}5\cdot 4200\cdot (57 - t_{\text{cb}})\)
\(\Rightarrow t_{\text{cb}} \approx 55\ ^\circ\text{C}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
Khối lượng nước đá tan do nhận nhiệt lượng từ dây nung là 14,6 g. |
|
S |
|
b |
Nhiệt nóng chảy riêng của nước đá thu được từ thí nghiệm trên xấp xỉ bằng 214 kJ/kg. |
|
S |
|
c |
Khối lượng nước đá còn lại sau khi bật biến áp nguồn được 2t (s) là 73,4 g. |
|
S |
|
d |
Khoảng thời gian từ khi bật biến áp nguồn đến khi nước đá vừa nóng chảy hoàn toàn xấp xỉ bằng 633 giây. |
Đ |
|
a) SAI
Khối lượng nước đá tan do nhận nhiệt từ môi trường trong khoảng thời gian t là:
$m_{\mathrm{mt}} = m_1 - m_0 = 12 - 5 = 7\ \mathrm{g}.$
Khối lượng nước đá tan do nhận nhiệt từ dây nung là:
$m_{\mathrm{dn}} = m_2 - m_1 - m_{\mathrm{mt}} = 26{,}6 - 12 - 7 = 7{,}6\ \mathrm{g}.$
b) SAI
Nhiệt nóng chảy riêng của nước đá thu được từ thí nghiệm trên là:
$\lvert Q_{\text{toả}}\rvert = \lvert Q_{\text{thu}}\rvert \Leftrightarrow P\cdot t = \lambda \cdot m_{\mathrm{dn}}
\Leftrightarrow \lambda = \dfrac{P\cdot t}{m_{\mathrm{dn}}}
= \dfrac{24\cdot 10^{5}}{7{,}6\cdot 10^{-3}} \approx 332\ \mathrm{kJ/kg}.$
c) SAI
Khối lượng nước đá còn lại sau khi bật biến áp nguồn được $2t$ (s) là:
$m = 100 - m_2 - (m_{\mathrm{mt}} + m_{\mathrm{dn}})
= 100 - 26{,}6 - (7 + 7{,}6) = 58{,}8\ \mathrm{g}.$
d) ĐÚNG
Khối lượng nước đá còn lại tại thời điểm bật biến áp nguồn: $m_{0t} = 100 - m_1 = 100 - 12 = 88\ \mathrm{g}.$
Xét trong khoảng thời gian từ khi bật biến áp nguồn đến khi nước đá vừa nóng chảy hoàn toàn ($t'$ (s)):
Khối lượng nước đá nóng chảy do nhận nhiệt từ môi trường là:
$m'_{\mathrm{mt}} = \dfrac{m_{\mathrm{mt}}\cdot t'}{t} = \dfrac{7}{105}\,t' = \dfrac{1}{15}\,t'\ (\mathrm{g}).$
Khối lượng nước đá nóng chảy do nhận nhiệt từ dây nung là:
$m'_{\mathrm{dn}} = \dfrac{m_{\mathrm{dn}}\cdot t'}{t} = \dfrac{7{,}6}{105}\,t'\ (\mathrm{g}).$
Khoảng thời gian $t'$ khi bật biến áp nguồn đến khi nước đá vừa nóng chảy hoàn toàn là:
$m'_{\mathrm{mt}} + m'_{\mathrm{dn}} = 88 \Leftrightarrow \dfrac{1}{15}\,t' + \dfrac{7{,}6}{105}\,t' = 88 \Rightarrow t' \approx 633\ \mathrm{s}.$
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
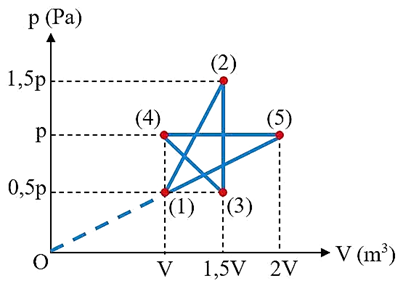
Nhiệt độ của khối khí helium ở trạng thái (1) xấp xỉ bằng 301 K. |
Đ |
|
|
b |
Từ trạng thái (2) sang trạng thái (3), khối khí thực hiện quá trình đẳng tích với nhiệt độ tuyệt đối tăng 3 lần. |
|
S |
|
c |
Từ trạng thái (3) sang trạng thái (4), nhiệt độ tuyệt đối cực đại mà khối khí có thể đạt được xấp xỉ bằng 602 K. |
Đ |
|
|
d |
Trong quá trình biến đổi trạng thái từ (4) – (5) – (1), nhiệt lượng khối khí helium tỏa ra môi trường là 2 500 J. |
Đ |
|
a) ĐÚNG
Nhiệt độ của khối khí ở trạng thái (1) là:
$p_1V_1=nRT_1 \Leftrightarrow T_1=\dfrac{p_1V_1}{nR}=\dfrac{0{,}5\cdot10^{6}\cdot5\cdot10^{-3}}{1\cdot8{,}31}\approx301\ \text{K}.$
b) SAI
Từ trạng thái (2) sang trạng thái (3), khối khí thực hiện quá trình đẳng tích nên nhiệt độ tuyệt đối tỉ lệ thuận với áp suất của khối khí. Từ đồ thị ta thấy áp suất của khối khí helium giảm 3 lần nên nhiệt độ tuyệt đối cũng giảm 3 lần.
c) ĐÚNG
Từ trạng thái (3) sang trạng thái (4), đồ thị biểu diễn sự biến thiên áp suất theo thể tích có dạng:
$p_x=aV_x+b.$
Tại trạng thái (3): $0{,}5p_a=a\cdot1{,}5V+b \Leftrightarrow 1{,}5\cdot5\cdot10^{-3}\,a+b=0{,}5\cdot10^{6}\quad(1)$
Tại trạng thái (4): $p_a=aV+b \Leftrightarrow 5\cdot10^{-3}\,a+b=10^{6}\quad(2)$
Từ (1) và (2) suy ra: $p_x=-2\cdot10^{8}\,V_x+2\cdot10^{6}.$
Mà $p_xV_x=nRT_x \Rightarrow T_x=\dfrac{p_xV_x}{nR}
=\dfrac{-2\cdot10^{8}}{8{,}31}V_x^{2}+\dfrac{2\cdot10^{6}}{8{,}31}V_x.$
Suy ra: $T_x'=\dfrac{-4\cdot10^{8}}{8{,}31}V_x+\dfrac{2\cdot10^{6}}{8{,}31}=0
\Rightarrow V_x=5\cdot10^{-3}\ \text{m}^3.$
Vậy từ trạng thái (3) sang (4), nhiệt độ tuyệt đối cực đại:
$T_{\max}=\dfrac{-2\cdot10^{8}}{8{,}31}(5\cdot10^{-3})^{2}
+\dfrac{2\cdot10^{6}}{8{,}31}(5\cdot10^{-3})\approx602\ \text{K}.$
d) ĐÚNG
Trong quá trình (4) – (5) – (1):
Công của khối khí:
$A_{451}=A_{45}+A_{51}
=-p_4\,(V_5-V_4)+\dfrac{1}{2}(p_5+p_1)(V_5-V_1)$
$\Rightarrow A_{451}=-p(2V-V)+\dfrac{1}{2}(p+0{,}5p)(2V-V)=-\dfrac{1}{4}pV.$
Độ biến thiên nội năng:
$\Delta U_{451}=U_1-U_4=\dfrac{3}{2}nRT_1-\dfrac{3}{2}nRT_4
=\dfrac{3}{2}(p_1V_1-p_4V_4)=\dfrac{3}{2}(0{,}5pV-pV)=-\dfrac{3}{4}pV.$
Theo nguyên lí I nhiệt động lực học:
$\Delta U_{451}=A_{451}+Q_{451}
\Rightarrow Q_{451}=\Delta U_{451}-A_{451}
=-\dfrac{1}{2}pV=-1\cdot10^{6}\cdot5\cdot10^{-3}=-2500\ \text{J}.$
Vậy trong quá trình (4) – (5) – (1), nhiệt lượng khối khí helium tỏa ra môi trường là $2\,500\ \text{J}$.
Câu 3
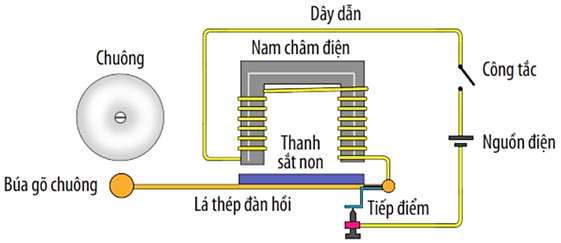
A. Chuông cửa hoạt động dựa trên hiện tượng cảm ứng điện từ.
B. Khi nhấn công tắc, thanh sắt non bị nam châm điện hút và dính chặt vào nam châm điện.
C. Khi ngắt công tắc, thanh sắt non bị nam châm điện đẩy ra khỏi nam châm điện.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
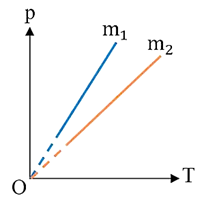
Câu 5
A. \(m_1 = 2m_2\).
B. \(m_1 = m_2\).
C. \(m_1 < m_2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.