Một robot tự hành ở một cảng vận chuyển công nghệ cao bắt đầu di chuyển từ vị trí nghỉ tại điểm A. Robot di chuyển như sau: Trong giai đoạn đầu, robot tăng tốc đều từ vận tốc \(0\,\,\left( {{\rm{m/s}}} \right)\) đến \(10\,\,\left( {{\rm{m/s}}} \right)\) trong thời gian chưa biết \({t_1}\)​ giây theo hàm số vận tốc \({v_1}\left( t \right) = at\) (\(a\) gọi là gia tốc trong giai đoạn này, \(a\,\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\)). Sau đó, robot tiếp tục di chuyển với vận tốc không đổi trong 40 giây. Cuối cùng, robot giảm tốc đều từ \(10\,\,\left( {{\rm{m/s}}} \right)\) và dừng lại đúng tại băng chuyền điểm \(B\) với thời gian \({t_2}\) giây theo hàm vận tốc \({v_2}\left( t \right) = 10 - bt\)(\(b\)gọi là gia tốc trong giai đoạn này, \(b\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\)). Toàn bộ quá trình vận chuyển diễn ra trong tổng thời gian là 70 giây.

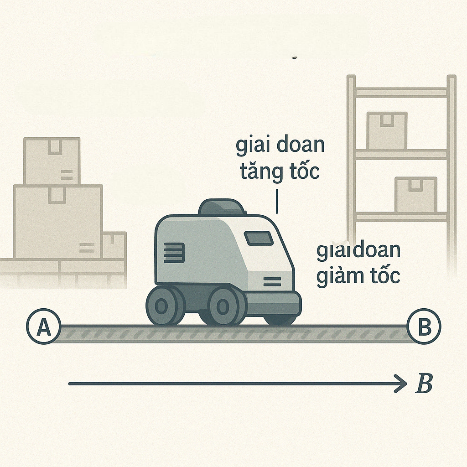
a) Nếu gia tốc \(a = 0,5\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\), thời gian tăng tốc \({t_1}\) bé hơn \(21\) giây.

b) Nếu gia tốc \(b = 0,8\,\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\), thời gian giảm tốc \({t_2}\) lớn hơn \(13\) giây.

c) \(a + b \le \,\frac{5}{4}\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\).

d) Tổng quãng đường mà robot đã di chuyển từ \(A\) đến \(B\) là \(550\,{\rm{m}}\).

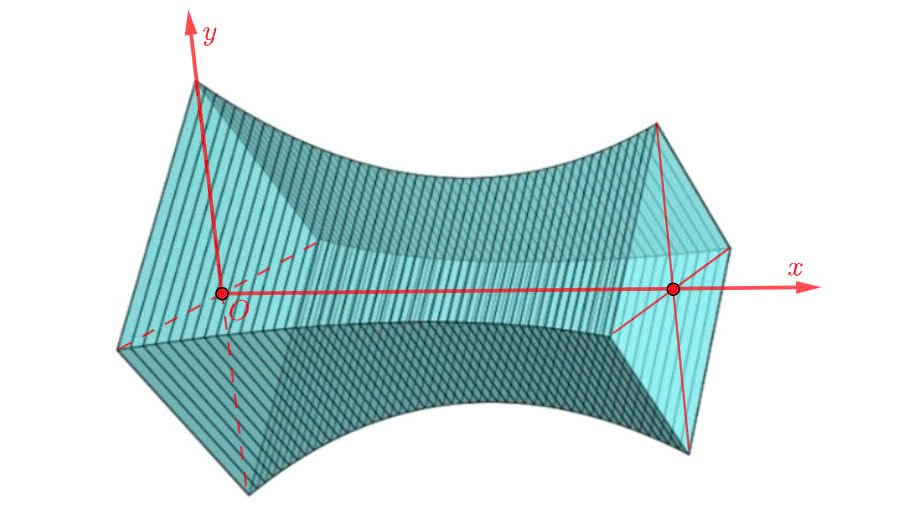
Chọn hệ trục toạ độ Oxy như hình vẽ.

Gọi \(L\left( x \right)\) là hàm biến thiên của độ dài đường chéo mặt cắt của toà nhà tại độ cao x.

Theo đề ta có, \(L\left( x \right)\)là một parabol đi qua ba điểm \(\left( {0;13\sqrt 2 } \right),\,\,\left( {30;10\sqrt 2 } \right),\,\,\left( {{x_o};\frac{{55\sqrt 2 }}{8}} \right)\) , trong đó \({x_o}\) là vị trí toà nhà có cạnh cạnh \({L_{min}} = 13,75\;{\rm{m}}{\rm{.}}\)

Ta có \(L\left( x \right) = a{\left( {x - {x_o}} \right)^2} + \frac{{55\sqrt 2 }}{8}\).

Ta có hệ: \(\left\{ \begin{array}{l}L\left( 0 \right) = a{\left( {0 - {x_o}} \right)^2} + \frac{{55\sqrt 2 }}{8} = 13\sqrt 2 \\L\left( {30} \right) = a{\left( {30 - {x_o}} \right)^2} + \frac{{55\sqrt 2 }}{8} = 10\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a{\left( {{x_o}} \right)^2} = \frac{{49\sqrt 2 }}{8}\\a{\left( {30 - {x_o}} \right)^2} = \frac{{25\sqrt 2 }}{8}\end{array} \right.\)

               \( \Rightarrow \frac{{{x_o}^2}}{{{{\left( {30 - {x_o}} \right)}^2}}} = \frac{{49}}{{25}} \Rightarrow \left[ \begin{array}{l}{x_o} = 105\,\left( L \right)\\{x_o} = 17,5\,\,\left( {TM} \right) \Rightarrow a = \frac{{\sqrt 2 }}{{50}}\end{array} \right.\,\)

Suy ra \(L\left( x \right) = \frac{{\sqrt 2 }}{{50}}{\left( {x - 17,5} \right)^2} + \frac{{55\sqrt 2 }}{8}\).

Do đó, diện tích thiết diện là \(S\left( x \right) = 2{\left[ {L\left( x \right)} \right]^2} = 2{\left[ {\frac{{\sqrt 2 }}{{50}}{{\left( {x - 17,5} \right)}^2} + \frac{{55\sqrt 2 }}{8}} \right]^2}\).

Vậy thể tích của toà nhà là \(\)\[V = \int\limits_0^{30} {S\left( x \right){\rm{d}}x}  = \int\limits_0^{30} {2{{\left[ {\frac{{\sqrt 2 }}{{50}}{{\left( {x - 17,5} \right)}^2} + \frac{{55\sqrt 2 }}{8}} \right]}^2}{\rm{d}}x}  \approx 8976\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].

Đáp án: 8976.

Gọi \({P_A}\left( t \right)\) là số lượng khách hàng luỹ kế của công ty A với \(t\) là số tháng kể từ khi ra mắt sản phẩm (\(t > 0\)).

Ta có \[{P_A}\left( t \right) = \int {f\left( t \right)dt = \int {\left( {2t + 7} \right)} } dt = {t^2} + 7t + C\].

Công ty A bắt đầu với 0 khách hàng nên \({P_A}\left( 0 \right) = 0 \Leftrightarrow {0^2} + 7.0 + C = 0 \Leftrightarrow C = 0\).

Vậy \[{P_A}\left( t \right) = {t^2} + 7t\].

Vì công ty B bắt đầu với 10 nghìn khách hàng đặt trước sản phẩm. Sau đó, họ duy trì một tốc độ thu hút khách hàng mới ổn định là 10 nghìn khách hàng/tháng, nên số lượng khách hàng lũy kế của công ty B sau \(t\) tháng ra mắt sản phẩm là \({P_B}\left( t \right) = 10 + 10t\) (\(t > 0\)).

Ta có \({P_A}\left( t \right) = {P_B}\left( t \right) \Leftrightarrow {t^2} + 7t = 10 + 10t \Leftrightarrow \left[ \begin{array}{l}t =  - 10\\t = 5\end{array} \right.\).

Vì \(t > 0\) nên \(t = 5\).

Vậy sau 5 tháng ra mắt, tổng số lượng khách hàng lũy kế của công ty A bằng tổng số lượng khách hàng lũy kế của công ty B (tính cả 10 nghìn khách hàng ban đầu).

Đáp án: 5.