Một kiến trúc sư chịu trách nhiệm thiết kế một tòa nhà cao 30 mét. Mặt cắt ngang tại mọi độ cao, vuông góc với trục thẳng đứng, luôn là một hình vuông (xem hình vẽ).
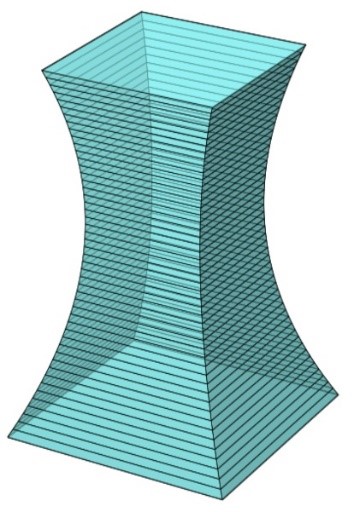
Mặt đáy tòa nhà là hình vuông có cạnh \({L_0} = 26\;{\rm{m,}}\) mặt đỉnh là hình vuông có cạnh \({L_{30}} = 20\;{\rm{m}}{\rm{.}}\)Mặt cắt ngang tại vị trí hẹp nhất của tòa nhà: Hình vuông có cạnh \({L_{min}} = 13,75\;{\rm{m}}{\rm{.}}\) Mặt cắt của tòa nhà theo mặt phẳng đứng chứa đường chéo đáy có dạng là hình phẳng giới hạn bởi hai đường cong parabol đối xứng nhau qua trục thẳng đứng đi qua tâm đáy của tòa nhà. Tính thể tích của tòa nhà đó (làm tròn đến hàng đơn vị, đơn vị tính: mét khối).
Một kiến trúc sư chịu trách nhiệm thiết kế một tòa nhà cao 30 mét. Mặt cắt ngang tại mọi độ cao, vuông góc với trục thẳng đứng, luôn là một hình vuông (xem hình vẽ).

Mặt đáy tòa nhà là hình vuông có cạnh \({L_0} = 26\;{\rm{m,}}\) mặt đỉnh là hình vuông có cạnh \({L_{30}} = 20\;{\rm{m}}{\rm{.}}\)Mặt cắt ngang tại vị trí hẹp nhất của tòa nhà: Hình vuông có cạnh \({L_{min}} = 13,75\;{\rm{m}}{\rm{.}}\) Mặt cắt của tòa nhà theo mặt phẳng đứng chứa đường chéo đáy có dạng là hình phẳng giới hạn bởi hai đường cong parabol đối xứng nhau qua trục thẳng đứng đi qua tâm đáy của tòa nhà. Tính thể tích của tòa nhà đó (làm tròn đến hàng đơn vị, đơn vị tính: mét khối).
Câu hỏi trong đề: Đề kiểm tra Toán 12 Chân trời sáng tạo Chương 4 có đáp án !!
Quảng cáo
Trả lời:
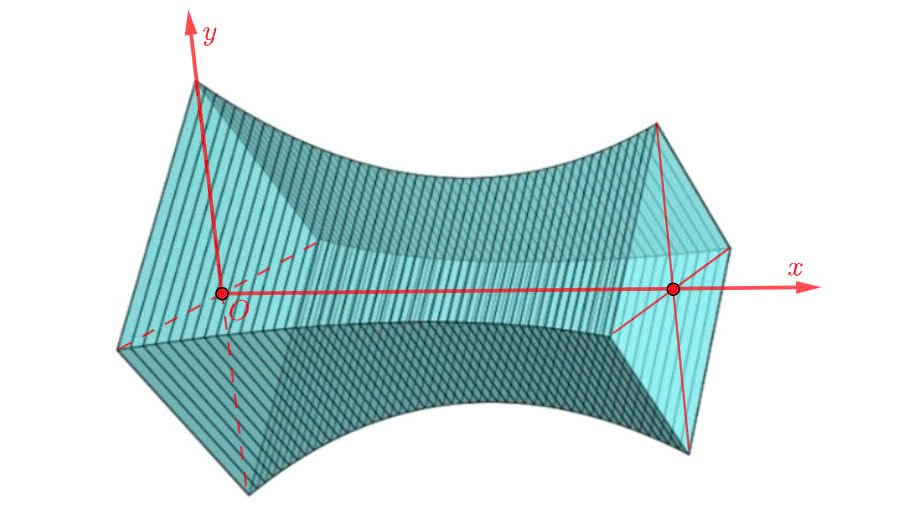
Chọn hệ trục toạ độ Oxy như hình vẽ.
Gọi \(L\left( x \right)\) là hàm biến thiên của độ dài đường chéo mặt cắt của toà nhà tại độ cao x.
Theo đề ta có, \(L\left( x \right)\)là một parabol đi qua ba điểm \(\left( {0;13\sqrt 2 } \right),\,\,\left( {30;10\sqrt 2 } \right),\,\,\left( {{x_o};\frac{{55\sqrt 2 }}{8}} \right)\) , trong đó \({x_o}\) là vị trí toà nhà có cạnh cạnh \({L_{min}} = 13,75\;{\rm{m}}{\rm{.}}\)
Ta có \(L\left( x \right) = a{\left( {x - {x_o}} \right)^2} + \frac{{55\sqrt 2 }}{8}\).
Ta có hệ: \(\left\{ \begin{array}{l}L\left( 0 \right) = a{\left( {0 - {x_o}} \right)^2} + \frac{{55\sqrt 2 }}{8} = 13\sqrt 2 \\L\left( {30} \right) = a{\left( {30 - {x_o}} \right)^2} + \frac{{55\sqrt 2 }}{8} = 10\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a{\left( {{x_o}} \right)^2} = \frac{{49\sqrt 2 }}{8}\\a{\left( {30 - {x_o}} \right)^2} = \frac{{25\sqrt 2 }}{8}\end{array} \right.\)
\( \Rightarrow \frac{{{x_o}^2}}{{{{\left( {30 - {x_o}} \right)}^2}}} = \frac{{49}}{{25}} \Rightarrow \left[ \begin{array}{l}{x_o} = 105\,\left( L \right)\\{x_o} = 17,5\,\,\left( {TM} \right) \Rightarrow a = \frac{{\sqrt 2 }}{{50}}\end{array} \right.\,\)
Suy ra \(L\left( x \right) = \frac{{\sqrt 2 }}{{50}}{\left( {x - 17,5} \right)^2} + \frac{{55\sqrt 2 }}{8}\).
Do đó, diện tích thiết diện là \(S\left( x \right) = 2{\left[ {L\left( x \right)} \right]^2} = 2{\left[ {\frac{{\sqrt 2 }}{{50}}{{\left( {x - 17,5} \right)}^2} + \frac{{55\sqrt 2 }}{8}} \right]^2}\).
Vậy thể tích của toà nhà là \(\)\[V = \int\limits_0^{30} {S\left( x \right){\rm{d}}x} = \int\limits_0^{30} {2{{\left[ {\frac{{\sqrt 2 }}{{50}}{{\left( {x - 17,5} \right)}^2} + \frac{{55\sqrt 2 }}{8}} \right]}^2}{\rm{d}}x} \approx 8976\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
Đáp án: 8976.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Ta có \(N'\left( 1 \right) = 18.1 - {3.1^2} = 15\) triệu tế bào/ml giờ.
b) Sai. Ta có \(\int {N'\left( t \right){\rm{d}}t} = \int {\left( {18t - 3{t^2}} \right){\rm{d}}t} = 9{t^2} - {t^3} + C\) (\(C \in \mathbb{R}\)).
c) Đúng. Ta có \(N\left( t \right) = 9{t^2} - {t^3} + C\) (\(C \in \mathbb{R}\)).
Mà \(N\left( 0 \right) = 10\) nên \(C = 10\). Vậy \(N\left( t \right) = 9{t^2} - {t^3} + 10\).
Tại thời điểm \(t = 6\), ta có \(N\left( 6 \right) = {9.6^2} - {6^3} + 10 = 118\). Ban đầu (\(t = 0\) giờ), mật độ vi khuẩn đo được là \(N\left( 0 \right) = 10\) triệu tế bào/ml nên tại thời điểm \(t = 6\), mật độ vi khuẩn đã tăng thêm 108 triệu tế bào/ml.
d) Đúng. Tại thời điểm \(t = 7\) giờ, ta có \(N\left( 7 \right) = {9.7^2} - {7^3} + 10 = 108\) nên mật độ vi khuẩn trong 1 ml sữa chua là 108 triệu tế bào/ml.
Lời giải
Lần tăng tốc đầu tiên xe chuyển động với vận tốc \(v\left( t \right) = a.t\), \(\left( {a > 0} \right)\).
Đến khi xe đạt vận tốc \({\rm{10}}\,{\rm{m/s}}\) thì xe chuyển động hết \({t_1} = \frac{{10}}{a}\,\left( {\rm{s}} \right)\).
Lần giảm tốc, xe chuyển động với vận tốc \({v_2} = 10 - bt\), \(\left( {b > 0} \right)\).
Khi xe dừng lại thì xe chuyển động thêm được \(10 - b{t_2} = 0 \Rightarrow {t_2} = \frac{{10}}{b}\left( {\rm{s}} \right)\).
Tổng thời gian hành trình: \({t_1} + 40 + {t_2} = 70 \Rightarrow \frac{{10}}{a} + \frac{{10}}{b} = 30 \Rightarrow \frac{1}{a} + \frac{1}{b} = 3\).
a) Đúng. Nếu gia tốc \(a = 0,5\,\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\), thời gian tăng tốc \({t_1} = \frac{{10}}{{0,5}} = 20\,\)giây < \(21\) giây.
b) Sai. Nếu gia tốc \(b = 0,8\,\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\), thời gian giảm tốc \({t_2} = \frac{{10}}{{0,8}} = 12,5\) giây < \(13\) giây.
c) Sai. Với \(a > 0,\,\,b > 0\), ta có bất đẳng thức: \(\left( {a + b} \right)\left( {\frac{1}{a} + \frac{1}{b}} \right) \ge 4\,\) mà \(\frac{1}{a} + \frac{1}{b} = 3\)nên \(a + b \ge \frac{4}{3}\).
Do đó \(a + b \le \,\frac{5}{4}\,\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\) là một đáp án sai.
d) Đúng. Quãng đường tăng tốc: \({S_1} = \int\limits_0^{{t_1}} {v\left( t \right){\rm{d}}t = \int\limits_0^{{t_1}} {at{\rm{d}}t} } = \frac{1}{2}a{\left( {{t_1}} \right)^2} = \frac{1}{2} \cdot \frac{{100}}{a} = \frac{{50}}{a}\,\,\left( {\rm{m}} \right)\) .
Quãng đường giảm tốc: \({S_2} = \int\limits_0^{{t_2}} {\left( {10 - bt} \right){\rm{d}}t} = 10{t_2} - \frac{1}{2}bt_2^2\).
Ta có \({t_2} = \frac{{10}}{b} \Rightarrow {S_2} = 10 \cdot \frac{{10}}{b} - \frac{1}{2}b{\left( {\frac{{10}}{b}} \right)^2} = \frac{{100}}{b} - \frac{{50}}{b} = \frac{{50}}{b}\,\left( {\rm{m}} \right)\).
Quãng đường chuyển động đều: \(10 \cdot 40 = 400\,{\mkern 1mu} \left( {\rm{m}} \right)\).
Tổng quãng đường:
\[S = {S_1} + 400 + {S_2} = \frac{{50}}{a} + 400{\mkern 1mu} + \frac{{50}}{b} = 50\left( {\frac{1}{a} + \frac{1}{b}} \right) + 400 = 150 + 400 = 550\,{\mkern 1mu} \left( {\rm{m}} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một hoa văn hình tròn tâm O, ngoại tiếp tam giác đều ABC có cạnh \[AB = 2\sqrt 3 \,{\rm{cm}}.\] Đường cong qua ba điểm A,B,C là một phần của parabol (xem hình vẽ). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/7-1759412289.png)
![Chọn C Diện tích hình vuông có cạnh là \(\sqrt {9 - {x^2}} \) là \[S = 9 - {x^2}\]. Thể tích của vật thể đó bằng \[\int\limits_0^3 {\left( {9 - {x^2}} \right)} \,{\rm{d}}x = \left. {\left( {9x - \frac{{{x^3}}}{3}} \right)} \right|_0^3 = 18\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/1-1759411506.png)
12A6 LN VÂN
Tại sao diện tích bằng 2 ×(L(x)^2 vậy a