Để trang trí cho một phòng trong một tòa nhà, người ta vẽ lên tường một hình như sau: trên mỗi cạnh của hình lục giác đều có cạnh bằng 2 dm có một cánh hoa hình parabol, đỉnh của parabol cách cạnh 3 dm và nằm phía ngoài hình lục giác, đường parabol đó đi qua hai đầu mút của mỗi cạnh (xem hình sau). Hãy tính diện tích của hình nói trên (kể cả hình lục giác đều) để mua sơn trang trí cho phù hợp (kết quả làm tròn đến chữ số thập phân thứ nhất sau dấu phẩy theo đơn vị decimet vuông).
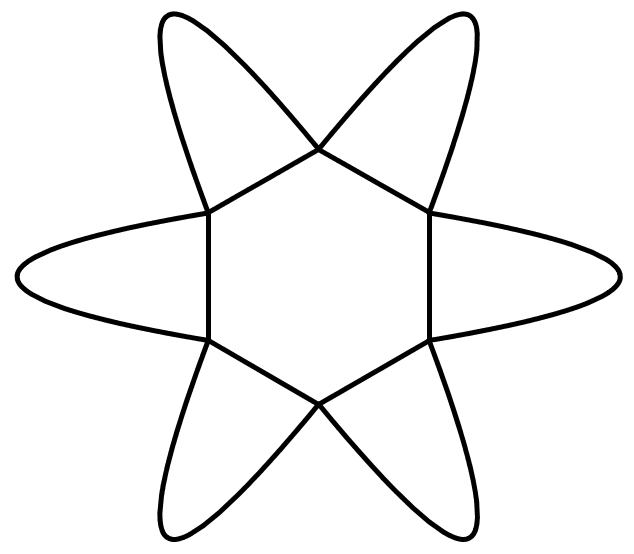
Để trang trí cho một phòng trong một tòa nhà, người ta vẽ lên tường một hình như sau: trên mỗi cạnh của hình lục giác đều có cạnh bằng 2 dm có một cánh hoa hình parabol, đỉnh của parabol cách cạnh 3 dm và nằm phía ngoài hình lục giác, đường parabol đó đi qua hai đầu mút của mỗi cạnh (xem hình sau). Hãy tính diện tích của hình nói trên (kể cả hình lục giác đều) để mua sơn trang trí cho phù hợp (kết quả làm tròn đến chữ số thập phân thứ nhất sau dấu phẩy theo đơn vị decimet vuông).
Câu hỏi trong đề: Bài tập ôn tập Toán 12 Chân trời sáng tạo Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hình lục giác đều có cạnh bằng 2 dm.
Diện tích của hình lục giác đều có thể được tính bằng công thức:
\({S_{{\rm{Luc}}\,\,{\rm{giac\;}}}} = \frac{{3\sqrt 3 }}{2}.{a^2}\) với \(a = 2{\rm{dm}}\).
Thay vào công thức ta có: \({S_{{\rm{Luc giac\;}}}} = \frac{{3\sqrt 3 }}{2}{.2^2} = 6\sqrt 3 \,\left( {{\rm{d}}{{\rm{m}}^2}} \right)\).
Chọn hệ trục tọa độ \(Oxy\) sao cho trung điểm của cạnh là \(AB\), với \(A\left( {1,0} \right),B\left( { - 1,0} \right)\) và đỉnh \(I\left( {0,3} \right)\) của parabol.
Phương trình của parabol có dạng: \(y = a{x^2} + b\).
Do parabol đi qua các điểm \(A\) và \(B\) nên ta có: \(y = - 3{x^2} + 3\).
Diện tích mỗi cánh hoa được tính bằng tích phân: \({S_{{\rm{C\'a nh\;hoa\;}}}} = \int\limits_{ - 1}^1 {\left( { - 3{x^2} + 3} \right){\rm{d}}x} \).
Tính tích phân: \({S_{{\rm{c\'a nh\;hoa\;}}}} = \left[ { - {x^3} + 3x} \right]\left| \begin{array}{l}1\\ - 1\end{array} \right. = \left( { - 1 + 3} \right) - \left( {1 - 3} \right) = 4{\rm{d}}{{\rm{m}}^2}\).
Hình có 6 cánh hoa nên tổng diện tích của các cánh hoa là:\({S_{{\rm{Tong c\'a nh\;hoa\;}}}} = 6.4 = 24\,\,{\rm{d}}{{\rm{m}}^2}\).
Tổng diện tích của hình bao gồm cả hình lục giác và các cánh hoa là:
\({S_{{\rm{Tong\;}}}} = {S_{{\rm{Luc\;gi\'a c\;}}}} + {S_{{\rm{Tong c\'a nh\;hoa\;\;}}}} = 6\sqrt 3 + 24 \approx 34,4\,{\rm{d}}{{\rm{m}}^2}\).
Đáp án: 34,4.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Sai. Ta có: \(\int {\left( {{t^2} - 8t} \right){\rm{d}}t} = \frac{{{t^3}}}{3} - 4{t^2} + C\).
b) Sai. Ta có: \(f'\left( t \right) > 0\,\,\)khi \(8 < t < 10\) và \(f'\left( t \right) < 0\,\,\)khi \(3 < t < 8\).
Nên số lượng vi sinh vật giảm trong khoảng từ 3 giờ đến 8 giờ, sau đó tăng dần trong khoảng 8 giờ đến 10 giờ.
c) Đúng. Bảng biến thiên của \(f\left( t \right)\):
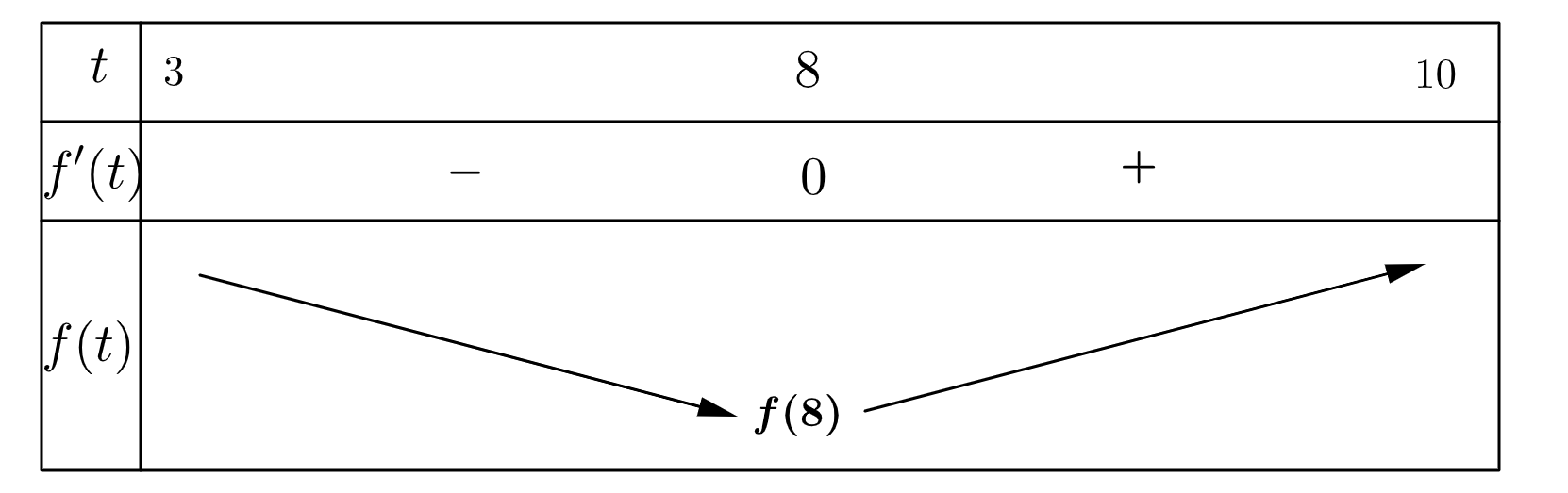
d) Đúng. \(f\left( t \right) = \frac{{{t^3}}}{3} - 4{t^2} + C\). Do \(f\left( 3 \right) = 50 \Rightarrow \frac{{{3^3}}}{3} - {4.3^2} + C = 50 \Rightarrow C = 77\).
Suy ra \(f\left( t \right) = \frac{1}{3}{t^3} - 4{t^2} + 77 \Rightarrow f\left( 6 \right) = 5\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
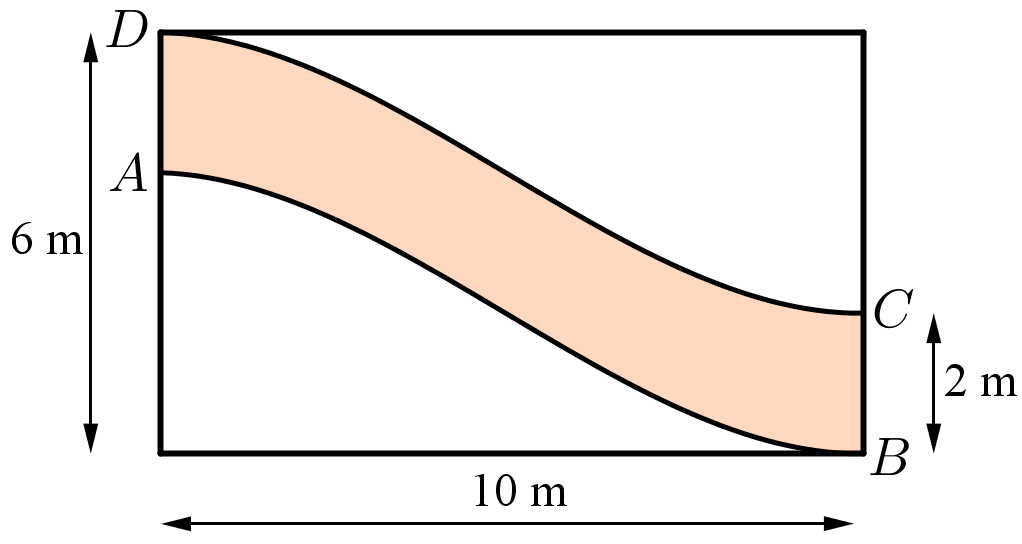
Để tính diện tích phần đổ bê tông, ta cần xác định diện tích giữa hai đường cong \(AB\) và \(DC\)
Đường cong DC là kết quả của việc tịnh tiến đường cong \(AB\) lên trên \(2\)m.
Giả sử hàm số của đường cong \(AB\) là \(f\left( x \right)\) thì hàm số của đường cong \(DC\) là \(f\left( x \right) + 2\).
Diện tích hình phẳng giới hạn bởi hai đường cong là: \[S = \int\limits_0^{10} {\left[ {f\left( x \right) + 2 - f\left( x \right)} \right]} {\rm{d}}x = 20\,{{\rm{m}}^2}\].
Lớp bê tông có độ dày là \(15\)cm tức là \(0,15\)m thì có thể tích là: \(20.0,15 = 3{{\rm{m}}^3}\).
Chi phí tổng cộng để đổ bê tông con đường đó là: \(3.1\,080\,000 = 3\,240\,000\) (đồng).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập