Nguyên hàm \(F\left( x \right)\) của hàm số \[f\left( x \right) = {\left( {2x - 3} \right)^2}\] thỏa mãn \(F\left( { - 1} \right) = - 17\) là
\[\frac{{{{\left( {2x - 3} \right)}^3}}}{3} + \frac{4}{3}\].
\[\frac{4}{3}{x^3} - 6{x^2} + 9x - \frac{2}{3}\].
\[\frac{4}{3}{x^3} - 6{x^2} + 9x + \frac{8}{3}\].
\[\frac{4}{3}{x^3} - 6{x^2} + 9x + \frac{2}{3}\].
Câu hỏi trong đề: Bài tập ôn tập Toán 12 Cánh diều Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng: B
Ta có \[\int {{{\left( {2x - 3} \right)}^2}{\rm{d}}x} = \int {\left( {4{x^2} - 12x + 9} \right){\rm{d}}x} = 4\int {{x^2}} {\rm{d}}x - 12\int {x{\rm{d}}x} + 9\int {{\rm{d}}x} = \frac{4}{3}{x^3} - 6{x^2} + 9x + C\].
\(F\left( { - 1} \right) = - 17 \Leftrightarrow \frac{4}{3}.{\left( { - 1} \right)^3} - 6.{\left( { - 1} \right)^2} + 9.\left( { - 1} \right) + C = - 17 \Leftrightarrow C = - \frac{2}{3}\).
Vậy nguyên hàm \(F\left( x \right)\) của hàm số \[f\left( x \right) = {\left( {2x - 3} \right)^2}\] thỏa mãn \(F\left( { - 1} \right) = - 17\) là\[\frac{4}{3}{x^3} - 6{x^2} + 9x - \frac{2}{3}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Sai. Chi phí mua 1 sản phẩm ứng với \(x = 0\), sau ra \(C = 5000.25 = 125\,000\) (đồng).
b) Đúng. Với \(x = 1\)ta có: \(C = 5000\left( {25 + 3\int\limits_0^1 {{t^{\frac{1}{4}}}{\rm{d}}t} } \right) = 137\,000\) (đồng).
Suy ra chi phí bảo trì năm đầu tiên của sản phẩm là \(137\,000 - 125\,000 = 12\,000\) (đồng).
c) Sai. Gọi \(x\)là số năm mà số tiền bảo trì bằng số tiền mua sản phẩm. Khi đó tổng số tiền mua và số tiền bảo trì là \(2 \cdot 125\,000 = 250\,000\).
\(5000\left( {25 + 3\int\limits_0^x {{t^{\frac{1}{4}}}{\rm{d}}t} } \right) = 250\,000 \Leftrightarrow 25 + 3\left( {\frac{4}{5}{t^{\frac{5}{4}}}|_0^x} \right) = 50 \Leftrightarrow \frac{{12}}{5}{x^{\frac{5}{4}}} = 25 \Leftrightarrow x = {\left( {\frac{{75}}{2}} \right)^{\frac{4}{5}}} \approx 6,52\) năm.
d) Sai. Số tiền mua và bảo trì 1 sản phẩm trong 10 năm là:
\(C = 5000\left( {25 + 3\int\limits_0^{10} {{t^{\frac{1}{4}}}{\rm{d}}t} } \right) = 5000\left( {25 + 24\sqrt[4]{{10}}} \right) \approx 338\,393,53\) (đồng).
Ta có: \(\frac{{10\,000\,000}}{{338\,393,53}} \approx 29,55\).
Vậy với 10 triệu đồng thì họ có thể mua và bảo trì tối đa 29 sản phẩm.
Lời giải
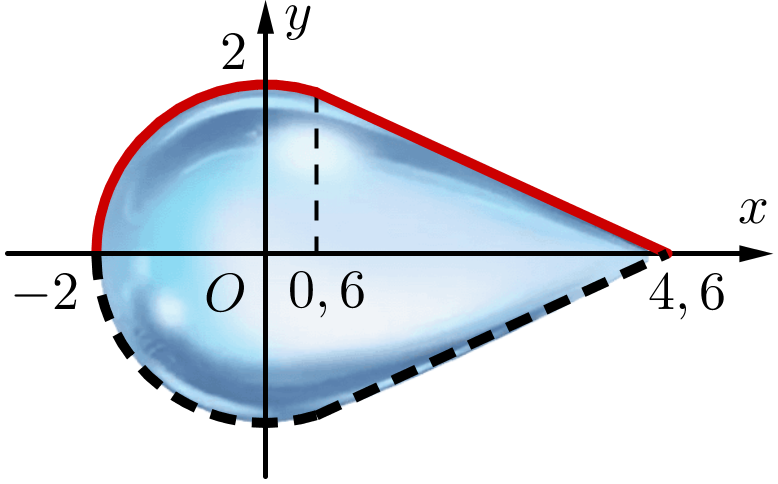
a) Đúng.\(\mathop {\lim }\limits_{x \to 0,{6^ - }} f\left( x \right) = \sqrt {4 - {{\left( {0,6} \right)}^2}} = \sqrt {4 - 0,36} = \sqrt {3,64} \approx 1,907\);
\(\mathop {\lim }\limits_{x \to 0,{6^ + }} f\left( x \right) = - \frac{{\sqrt {91} }}{{20}}.0,6 + \frac{{23\sqrt {91} }}{{100}} \approx 1,907\).
Vậy hàm số \(y = f\left( x \right)\) liên tục tại \(x = 0,6\).
b) Đúng.Diện tích mặt cắt của giọt nước thủy tinh khi cắt bởi mặt phẳng qua trục được tính bởi công thức \[S = 2\int\limits_{ - 2}^{4,6} {f\left( x \right){\rm{d}}x} \] cm2.
c) Sai. Thể tích của giọt nước thủy tinh này là:
\[V = {V_1} + {V_2} = \pi \int\limits_{ - 2}^{0,6} {{{\left( {\sqrt {4 - {x^2}} } \right)}^2}{\rm{d}}x + } \,\pi \int\limits_{0,6}^{4,6} {{{\left( { - \frac{{\sqrt {91} }}{{20}}x + \frac{{23\sqrt {91} }}{{100}}} \right)}^2}{\rm{d}}x} = \frac{{4693\pi }}{{375}} \approx 39,32\] cm3.
d) Đúng. Khối lượng của giọt nước thủy tinh này là: \(m = \rho .V = 2,6.\frac{{4693\pi }}{{375}} \approx 102,22\)g.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.