Chị Hồng đang lái xe với vận tốc \(5{\rm{\;m}}/{\rm{s}}\) thì nhận thấy phía trước đèn giao thông đang chuẩn bị chuyển sang đèn đỏ nên cần giảm tốc độ của xe để đợi đèn đỏ. Sau khi đạp phanh, xe chuyển động chậm dần đều với vận tốc \(v\left( t \right) = - 0,5t + 5\left( {{\rm{\;m}}/{\rm{s}}} \right)\), trong đó \(t\) là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến khi xe dừng hẳn, xe di chuyển quãng đường bao nhiêu mét?
Câu hỏi trong đề: Bài tập ôn tập Toán 12 Cánh diều Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Đáp án:
Lúc đạp phanh tại thời điểm: \[v = 5 \Rightarrow - 0,5{t_1} + 5 = 5 \Leftrightarrow {t_1} = 0\] giây.
Xe dừng ở thời điểm \[v = 0 \Leftrightarrow - 0,5{t_2} + 5 = 0 \Leftrightarrow {t_2} = 10\] giây.
Khi đó quãng đường xe di chuyển là: \[S = \int\limits_0^{10} {\left( { - 0,5t + 5} \right){\rm{d}}t} = 25\] mét.
Đáp án: 25.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Sai. Chi phí mua 1 sản phẩm ứng với \(x = 0\), sau ra \(C = 5000.25 = 125\,000\) (đồng).
b) Đúng. Với \(x = 1\)ta có: \(C = 5000\left( {25 + 3\int\limits_0^1 {{t^{\frac{1}{4}}}{\rm{d}}t} } \right) = 137\,000\) (đồng).
Suy ra chi phí bảo trì năm đầu tiên của sản phẩm là \(137\,000 - 125\,000 = 12\,000\) (đồng).
c) Sai. Gọi \(x\)là số năm mà số tiền bảo trì bằng số tiền mua sản phẩm. Khi đó tổng số tiền mua và số tiền bảo trì là \(2 \cdot 125\,000 = 250\,000\).
\(5000\left( {25 + 3\int\limits_0^x {{t^{\frac{1}{4}}}{\rm{d}}t} } \right) = 250\,000 \Leftrightarrow 25 + 3\left( {\frac{4}{5}{t^{\frac{5}{4}}}|_0^x} \right) = 50 \Leftrightarrow \frac{{12}}{5}{x^{\frac{5}{4}}} = 25 \Leftrightarrow x = {\left( {\frac{{75}}{2}} \right)^{\frac{4}{5}}} \approx 6,52\) năm.
d) Sai. Số tiền mua và bảo trì 1 sản phẩm trong 10 năm là:
\(C = 5000\left( {25 + 3\int\limits_0^{10} {{t^{\frac{1}{4}}}{\rm{d}}t} } \right) = 5000\left( {25 + 24\sqrt[4]{{10}}} \right) \approx 338\,393,53\) (đồng).
Ta có: \(\frac{{10\,000\,000}}{{338\,393,53}} \approx 29,55\).
Vậy với 10 triệu đồng thì họ có thể mua và bảo trì tối đa 29 sản phẩm.
Lời giải
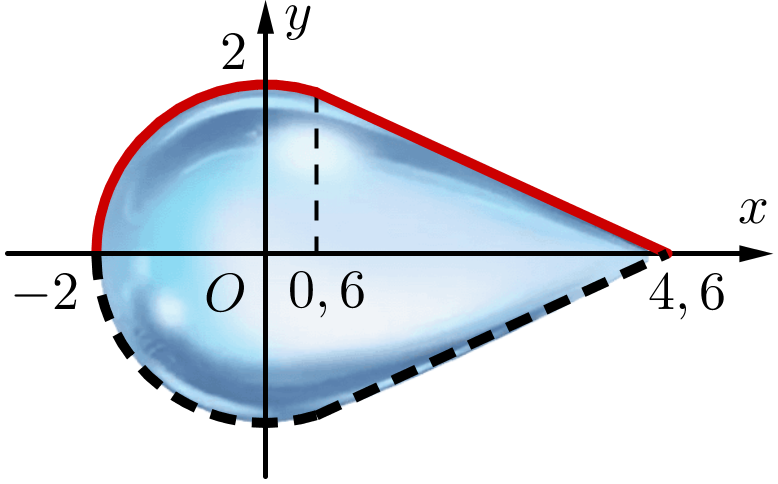
a) Đúng.\(\mathop {\lim }\limits_{x \to 0,{6^ - }} f\left( x \right) = \sqrt {4 - {{\left( {0,6} \right)}^2}} = \sqrt {4 - 0,36} = \sqrt {3,64} \approx 1,907\);
\(\mathop {\lim }\limits_{x \to 0,{6^ + }} f\left( x \right) = - \frac{{\sqrt {91} }}{{20}}.0,6 + \frac{{23\sqrt {91} }}{{100}} \approx 1,907\).
Vậy hàm số \(y = f\left( x \right)\) liên tục tại \(x = 0,6\).
b) Đúng.Diện tích mặt cắt của giọt nước thủy tinh khi cắt bởi mặt phẳng qua trục được tính bởi công thức \[S = 2\int\limits_{ - 2}^{4,6} {f\left( x \right){\rm{d}}x} \] cm2.
c) Sai. Thể tích của giọt nước thủy tinh này là:
\[V = {V_1} + {V_2} = \pi \int\limits_{ - 2}^{0,6} {{{\left( {\sqrt {4 - {x^2}} } \right)}^2}{\rm{d}}x + } \,\pi \int\limits_{0,6}^{4,6} {{{\left( { - \frac{{\sqrt {91} }}{{20}}x + \frac{{23\sqrt {91} }}{{100}}} \right)}^2}{\rm{d}}x} = \frac{{4693\pi }}{{375}} \approx 39,32\] cm3.
d) Đúng. Khối lượng của giọt nước thủy tinh này là: \(m = \rho .V = 2,6.\frac{{4693\pi }}{{375}} \approx 102,22\)g.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.