Một cái cổng hình Parabol như hình vẽ sau:
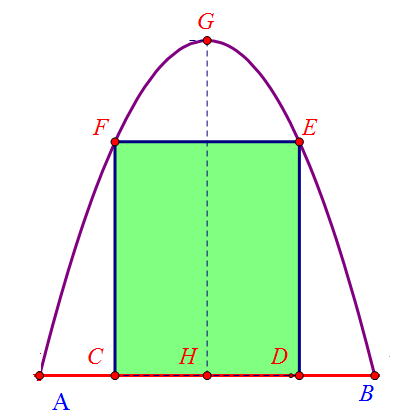
Chiều cao \(GH = 4\,{\rm{m}}\), chiều rộng \(AB = 4\,{\rm{m}}\), \(AC = BD = 0,9\,{\rm{m}}\). Chủ nhà làm hai cánh cổng nhựa lõi thép UPVC, khi đóng lại là hình chữ nhật \(CDEF\) tô đậm có giá là \(1\,500\,000\) đồng/m2, còn các phần để trắng làm xiên hoa có giá là \(1\,000\,000\)đồng/m2. Tổng số tiền để làm hai phần nói trên là bao nhiêu triệu đồng? (kết quả làm tròn đến hàng phần chục).
Câu hỏi trong đề: Đề kiểm tra Toán 12 Cánh diều Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Đáp án:
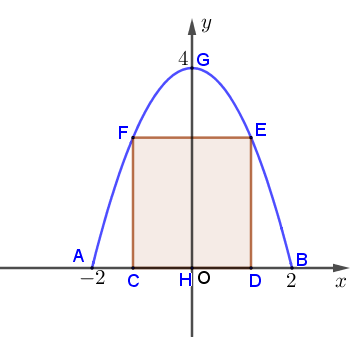
Đặt hệ trục \(Oxy\) như hình vẽ.
Gọi PT Parabol có dạng: \(\left( P \right):\,\,y = a{x^2} + bx + c\).
\(\left( P \right)\) có đỉnh \(G\left( {0;\,4} \right)\) và đi qua \(B\left( {2;\,0} \right)\) suy ra: \(a = - 1;\,b = 0;\,c = 4\)\( \Rightarrow \left( P \right):\,\,y = - {x^2} + 4\).
Ta có: \({x_E} = {x_D} = 1,1 \Rightarrow {y_E} = - 1,{1^2} + 4 = 2,79\)\( \Rightarrow ED = 2,79\).
\({S_{CDEF}} = CD.DF = 2,2.2,79 = 6,138\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Diện tích hình phẳng giới hạn bởi Parabol \(\left( P \right)\) và trục hoành là
\({S_{\left( P \right)}} = \int\limits_{ - 2}^2 {\left( { - {x^2} + 4} \right)} = \frac{{32}}{3}\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Suy ra diện tích làm xiên hoa là: \(S = {S_{\left( P \right)}} - {S_{CDEF}} = \frac{{6793}}{{1500}}\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Đổi đơn vị: \(1\,500\,000\) đồng/m2 \( = 1\,,5\) triệu đồng/m2, \(1\,000\,000\)đồng/m2 \( = 1\,\)triệuđồng/m2.
Tổng số tiền để làm hai phần nói trên là:
\(T = 6,138.1,5 + \frac{{6793}}{{1500}}.1 \approx 13,7\) (triệu đồng).
Đáp án: 13,7.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
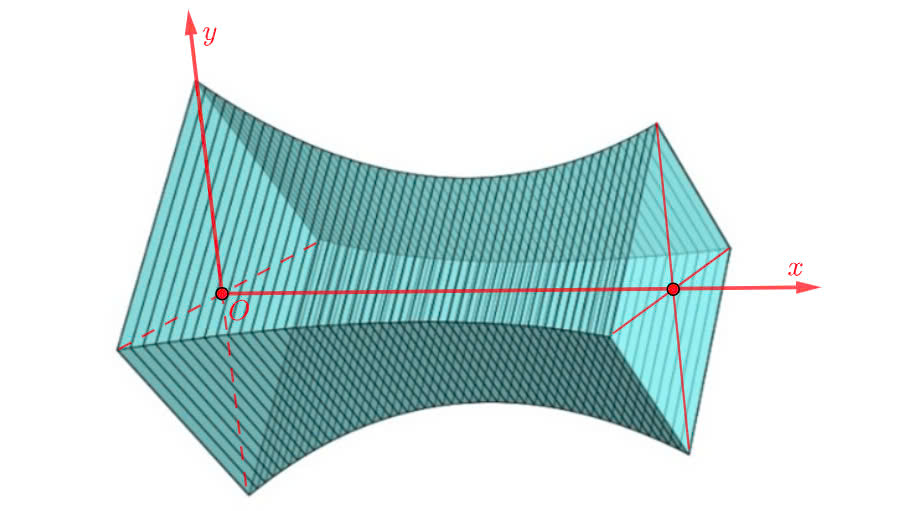
Chọn hệ trục toạ độ Oxy như hình vẽ.
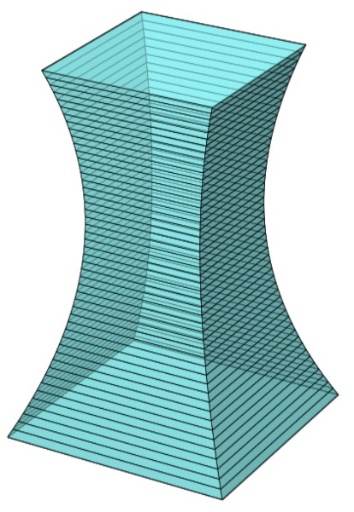
Gọi \(L\left( x \right)\) là hàm biến thiên của độ dài đường chéo mặt cắt của toà nhà tại độ cao x.
Theo đề ta có, \(L\left( x \right)\)là một parabol đi qua ba điểm \(\left( {0;13\sqrt 2 } \right),\,\,\left( {30;10\sqrt 2 } \right),\,\,\left( {{x_o};\frac{{55\sqrt 2 }}{8}} \right)\) , trong đó \({x_o}\) là vị trí toà nhà có cạnh cạnh \({L_{min}} = 13,75\;{\rm{m}}{\rm{.}}\)
Ta có \(L\left( x \right) = a{\left( {x - {x_o}} \right)^2} + \frac{{55\sqrt 2 }}{8}\).
Ta có hệ: \(\left\{ \begin{array}{l}L\left( 0 \right) = a{\left( {0 - {x_o}} \right)^2} + \frac{{55\sqrt 2 }}{8} = 13\sqrt 2 \\L\left( {30} \right) = a{\left( {30 - {x_o}} \right)^2} + \frac{{55\sqrt 2 }}{8} = 10\sqrt 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a{\left( {{x_o}} \right)^2} = \frac{{49\sqrt 2 }}{8}\\a{\left( {30 - {x_o}} \right)^2} = \frac{{25\sqrt 2 }}{8}\end{array} \right.\)
\( \Rightarrow \frac{{{x_o}^2}}{{{{\left( {30 - {x_o}} \right)}^2}}} = \frac{{49}}{{25}} \Rightarrow \left[ \begin{array}{l}{x_o} = 105\,\left( L \right)\\{x_o} = 17,5\,\,\left( {TM} \right) \Rightarrow a = \frac{{\sqrt 2 }}{{50}}\end{array} \right.\,\)
Suy ra \(L\left( x \right) = \frac{{\sqrt 2 }}{{50}}{\left( {x - 17,5} \right)^2} + \frac{{55\sqrt 2 }}{8}\).
Do đó, diện tích thiết diện là \(S\left( x \right) = 2{\left[ {L\left( x \right)} \right]^2} = 2{\left[ {\frac{{\sqrt 2 }}{{50}}{{\left( {x - 17,5} \right)}^2} + \frac{{55\sqrt 2 }}{8}} \right]^2}\).
Vậy thể tích của toà nhà là \(\)\[V = \int\limits_0^{30} {S\left( x \right){\rm{d}}x} = \int\limits_0^{30} {2{{\left[ {\frac{{\sqrt 2 }}{{50}}{{\left( {x - 17,5} \right)}^2} + \frac{{55\sqrt 2 }}{8}} \right]}^2}{\rm{d}}x} \approx 8976\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
Đáp án: 8976.
Lời giải
Khi xe dừng hẳn thì vận tốc bằng 0, do đó \( - 4t + 20 = 0 \Leftrightarrow t = 5\) (giây).
Từ lúc giảm ga và kéo phanh đến khi dừng hẳn, mô tô di chuyển được quãng đường là:
\(S = \int\limits_0^5 {v\left( t \right){\rm{d}}t} = \int\limits_0^5 {\left( { - 4t + 20} \right){\rm{d}}t} = 50\) (mét).
Đáp án: 50.
Câu 3
\(f\left( 2 \right) = - 4\).
\(f\left( 2 \right) = - 2\).
\(f\left( 2 \right) = 4\).
\(f\left( 2 \right) = - 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
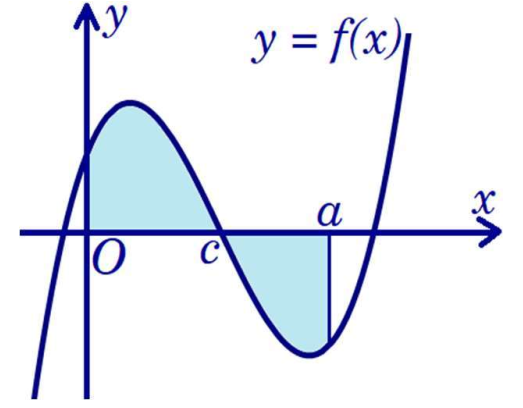
\(S = \int\limits_0^c {f\left( x \right){\rm{d}}x} - \int\limits_a^c {f\left( x \right){\rm{d}}x} \).
\(S = - \int\limits_0^a {f\left( x \right){\rm{d}}x} \).
\(S = - \int\limits_0^c {f\left( x \right){\rm{d}}x} + \int\limits_a^c {f\left( x \right){\rm{d}}x} \).
\(S = \int\limits_0^c {f\left( x \right){\rm{d}}x} + \int\limits_a^c {f\left( x \right){\rm{d}}x} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\(F\left( x \right) = - {e^x} - 2\cos x + 23\).
\(F\left( x \right) = {e^x} - 2\cos x + 21\).
\(F\left( x \right) = {e^x} + 2\cos x + 17\).
\(F\left( x \right) = {e^x} + 2\sin x + 19\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.