Đề kiểm tra Toán 12 Cánh diều Chương 4 có đáp án - Đề 1
28 người thi tuần này 4.6 230 lượt thi 11 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
\({f_3}\left( x \right) = - \frac{1}{2}\cos 2x\).
\({f_4}\left( x \right) = - \frac{1}{4}\cos 2x\).
\({f_2}\left( x \right) = \cos 2x\).
\({f_1}\left( x \right) = - \cos 2x\).
Lời giải
Đáp án đúng: C
Ta có \({\left( {\frac{1}{2}\sin 2x} \right)^\prime } = \cos 2x\).
Câu 2
\(F\left( x \right) = - {e^x} - 2\cos x + 23\).
\(F\left( x \right) = {e^x} - 2\cos x + 21\).
\(F\left( x \right) = {e^x} + 2\cos x + 17\).
\(F\left( x \right) = {e^x} + 2\sin x + 19\).
Lời giải
Đáp án đúng:B
\(F\left( x \right) = \int {f\left( x \right){\rm{d}}x = \int {\left( {{e^x} + 2\sin x} \right)} } \,{\rm{d}}x = {e^x} - 2\cos x + C\)
Mà \(F\left( 0 \right) = 20 \Leftrightarrow {e^0} - 2\cos 0 + C = 20 \Leftrightarrow C = 21\) .
Vậy \(F\left( x \right) = {e^x} - 2\cos x + 21\).
Lời giải
Đáp án đúng:D
\(\int\limits_1^2 {\left[ {f(x) + g(x)} \right]{\rm{d}}x} \)\( = \int\limits_1^2 {f(x){\rm{d}}x} + \int\limits_1^2 {g(x){\rm{d}}x} \)\( = 3 + 2 = 5\).
Câu 4
\(f\left( 2 \right) = - 4\).
\(f\left( 2 \right) = - 2\).
\(f\left( 2 \right) = 4\).
\(f\left( 2 \right) = - 3\).
Lời giải
Đáp án đúng:B
Ta có:\(\int\limits_0^2 {f'\left( x \right){\rm{d}}x = - 3} \Leftrightarrow f\left( 2 \right) - f\left( 0 \right) = - 3 \Leftrightarrow f\left( 2 \right) = - 3 + f\left( 0 \right) = - 3 + 1 = - 2\).
Câu 5
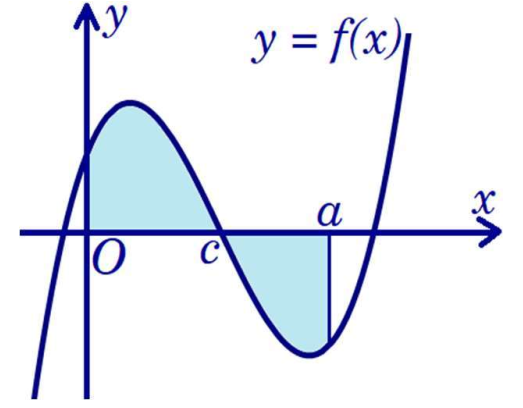
\(S = \int\limits_0^c {f\left( x \right){\rm{d}}x} - \int\limits_a^c {f\left( x \right){\rm{d}}x} \).
\(S = - \int\limits_0^a {f\left( x \right){\rm{d}}x} \).
\(S = - \int\limits_0^c {f\left( x \right){\rm{d}}x} + \int\limits_a^c {f\left( x \right){\rm{d}}x} \).
\(S = \int\limits_0^c {f\left( x \right){\rm{d}}x} + \int\limits_a^c {f\left( x \right){\rm{d}}x} \).
Lời giải
Đáp án đúng:A
Diện tích hình phẳng: \[S = \int\limits_0^a {\left| {f\left( x \right)} \right|{\rm{d}}x} = \int\limits_0^c {\left| {f\left( x \right)} \right|{\rm{d}}x} + \int\limits_c^a {\left| {f\left( x \right)} \right|{\rm{d}}x} = \int\limits_0^c {f\left( x \right){\rm{d}}x} - \int\limits_a^c {f\left( x \right){\rm{d}}x} \].
Câu 6
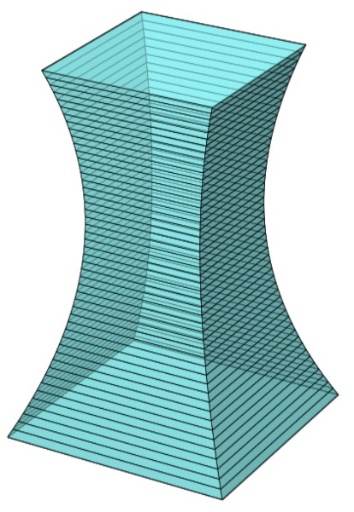
\(V = \frac{{406}}{{15}}\).
\(V = \frac{{406}}{{15}}\pi \).
\(V = \frac{{22}}{3}\pi \).
\(V = \frac{{512}}{{15}}\pi \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.