9 bài tập Tổng và hiệu của hai vectơ (có lời giải)
29 người thi tuần này 4.6 173 lượt thi 8 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
Lời giải
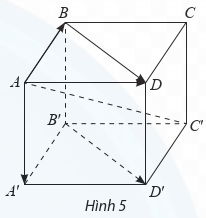
a) \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \); \(\overrightarrow {{A^\prime }{B^\prime }} + \overline {{B^\prime }{C^\prime }} = \overline {{A^\prime }{C^\prime }} {\rm{. }}\)
b) Vî AA'B'B là hình bình hành, suy ra \(AB//{A^\prime }{B^\prime }\) và \(AB = {A^\prime }{B^\prime }\).
Ta có hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {{A^\prime }{B^\prime }} \) cùng hướng và có độ dài bằng nhau nên \(\overrightarrow {AB} = \overrightarrow {{A^\prime }{B^\prime }} \). Tương tự: \(\overrightarrow {BC} = \overrightarrow {{B^\prime }{C^\prime }} ;\overrightarrow {AC} = \overrightarrow {{A^\prime }{C^\prime }} \).
c) Vì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) và \(\overrightarrow {{A^\prime }{B^\prime }} + \overrightarrow {{B^\prime }{C^\prime }} = \overrightarrow {{A^\prime }{C^\prime }} \) mà \(\overrightarrow {AC} = \overrightarrow {{A^\prime }{C^\prime }} \) nên \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {{A^\prime }{B^\prime }} + \overrightarrow {{B^\prime }{C^\prime }} \).
Lời giải
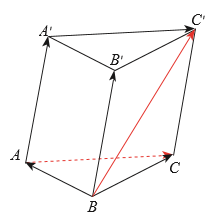
Ta có \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) là hình lăng trụ nên \(A{A^\prime }{C^\prime }C\) là hình bình hành, suy ra \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Do đó \(\overrightarrow {BA} + \overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \).
Tương tự, ta cūng có \(A{A^\prime }{B^\prime }B\) là hình bình hành, suy ra \(\overrightarrow {A{A^\prime }} = \overrightarrow {B{B^\prime }} \).
Do đó \(\overrightarrow {BC} + \overrightarrow {A{A^\prime }} = \overrightarrow {BC} + \overrightarrow {B{B^\prime }} = \overrightarrow {B{C^\prime }} \)
Lời giải
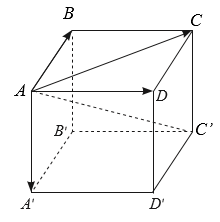
a) Do ABCD là hình bình hành nên \(\overrightarrow {AD} = \overrightarrow {BC} \).
Do đó \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
Tương tự. AA' \({C^\prime }{\rm{C}}\) là hình bình hành nên \(\overrightarrow {A{A^\prime }} = \overrightarrow {C{C^\prime }} \).
Do đó \(\overrightarrow {AC} + \overrightarrow {A{A^\prime }} = \overrightarrow {AC} + \overrightarrow {C{C^\prime }} = \overrightarrow {A{C^\prime }} \).
b) Có \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A^\prime }} = \overrightarrow {AC} + \overrightarrow {A{A^\prime }} = \overrightarrow {A{C^\prime }} \)
Lời giải
a) Theo quy tắc hình hộp, ta có \(\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CG} = \overrightarrow {CE} \).
b) Vì ABCD.EFGH là hình hộp nên theo quy tắc hình hộp ta có:
\(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} = \overrightarrow {DF} \)
c) Ta có \(\overrightarrow {CG} = \overrightarrow {AE} ,\overrightarrow {EH} = \overrightarrow {AD} \).
Suy ra: \(\overrightarrow {AB} + \overrightarrow {CG} + \overrightarrow {EH} = \overrightarrow {AB} + \overrightarrow {AE} + \overrightarrow {AD} \).
Theo quy tắc hình hộp, ta có \(\overrightarrow {AB} + \overrightarrow {AE} + \overrightarrow {AD} = \overrightarrow {AG} \).
Vậy \(\overrightarrow {AB} + \overrightarrow {CG} + \overrightarrow {EH} = \overrightarrow {AG} \).
d) Vì DCGH là hình bình hành nên \(\overrightarrow {GC} = \overrightarrow {HD} \).
Tương tự \({\rm{ABGH}}\) là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {HG} \).
Do đó \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} = \overrightarrow {HE} + \overrightarrow {HD} + \overrightarrow {HG} = \overrightarrow {HB} \) (theo quy tắc hình hộp).
Lời giải
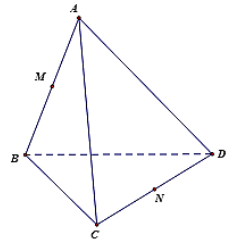
a) \(\overrightarrow {BM} + \overrightarrow {AC} + \overrightarrow {ND} = \overrightarrow {BM} + \overrightarrow {AM} + \overrightarrow {MC} + \overrightarrow {ND} = \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {ND} = \overrightarrow {MN} \)
(Do \(M\) và \(N\) lần lượt là trung điếm của AB và CD nên \(\overrightarrow {NC} + \overrightarrow {ND} = \vec 0;\overrightarrow {BM} + \overrightarrow {AM} = \vec 0\) ).
b) \(\overrightarrow {AD} - \overrightarrow {AM} + \overrightarrow {NC} = \overrightarrow {MD} + \overrightarrow {NC} = \overrightarrow {MN} + \overrightarrow {ND} + \overrightarrow {NC} = \overrightarrow {MN} (\) vì \(\overrightarrow {ND} + \overrightarrow {NC} = \vec 0)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.