5 bài tập Tọa độ của điểm, vectơ (có lời giải)
36 người thi tuần này 4.6 145 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
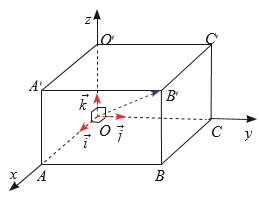
Ta có: \(\overrightarrow {OA} = 4\vec i + 0\vec j + 0\vec k\), suy ra \(A(4;0;0)\);
\(\overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {OC} = 4\vec i + 6\vec j + 0\vec k{\rm{, suy ra }}B(4;6;0);\)
\({\rm{ }}\overrightarrow {O{B^\prime }} = \overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {O{O^\prime }} = 4\vec i + 6\vec j + 3\vec k{\rm{, suy ra }}{B^\prime }(4;6;3)\)
Lời giải
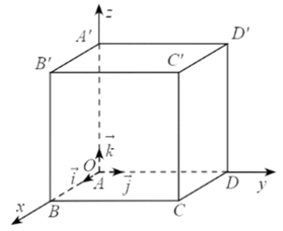
Vì \(\overrightarrow {OB} \) và \(\vec i\) cùng hướng và \({\rm{OB}} = 5\) nên \(\overrightarrow {OB} = 5\vec i\).
Tương tự, ta có \(\overrightarrow {OD} = 5\vec j;\overrightarrow {O{A^\prime }} = 5\vec k\).
Theo quy tắc hình bình hành, ta có: \(\overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} = 5\vec i + 5\vec j\).
Theo quy tắc hình hộp, ta có: \(\overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} + \overrightarrow {O{A^\prime }} = 5\vec i + 5\vec j + 5\vec k\).
Do đó \({\rm{B}}(5;0;0),{\rm{C}}(5;5;0),{{\rm{C}}^\prime }(5;5;5)\).
Lời giải
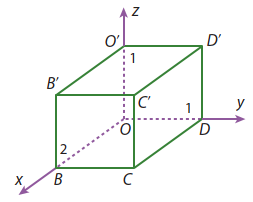
Ta cần tìm toạ độ các đỉnh \(O,C,{B^\prime },{C^\prime },{D^\prime }\).
- Toạ độ đỉnh \(O\) là \((0;0;0)\).
- Theo giả thiết, ta có \(\overrightarrow {OB} = 2\vec i,\overrightarrow {OD} = \vec j,\overrightarrow {O{O^\prime }} = \vec k\).
Suy ra:
\(\overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} = 2\vec i + \vec j;\overrightarrow {O{B^\prime }} = \overrightarrow {OB} + \overrightarrow {O{O^\prime }} = 2\vec i + \vec k;\)
\(\overrightarrow {O{C^\prime }} = \overrightarrow {OB} + \overrightarrow {OD} + \overrightarrow {O{O^\prime }} = 2\vec i + \vec j + \vec k;{\rm{ }}\overrightarrow {O{D^\prime }} = \overrightarrow {OD} + \overrightarrow {O{O^\prime }} = \vec j + \vec k.\)
Vậy \(C(2;1;0),{B^\prime }(2;0;1),{C^\prime }(2;1;1),{D^\prime }(0;1;1)\).
Lời giải
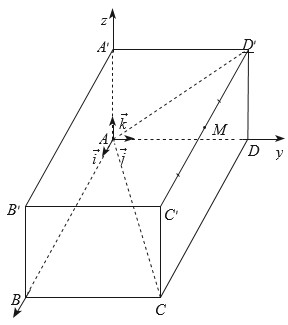
Để tìm tọa độ của vectơ \(\overrightarrow {AB} \), ta cần biểu diễn \(\overrightarrow {AB} \) theo ba vectơ \(\vec i,\vec j,\vec k\).
Do \(\overrightarrow {AB} \) cùng hướng với \(\vec i\) và \(|\overrightarrow {AB} | = AB = 8 = 8|\vec i|\) nên \(\overrightarrow {AB} = 8\vec i\) hay \(\overrightarrow {AB} = 8\vec i + 0\vec j + 0\vec k\).
Tương tự, ta cũng có: \(\overrightarrow {AD} = 0\vec i + 6\vec j + 0\vec k,\overrightarrow {A{A^\prime }} = 0\vec i + 0\vec j + 4\vec k\).
Trong hình bình hành ABCD, ta có: \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} = 8\vec i + 6\vec j + 0\vec k\).
Trong hình bình hành \(A{A^\prime }{C^\prime }C\), ta có: \(\overrightarrow {A{C^\prime }} = \overrightarrow {AC} + \overrightarrow {A{A^\prime }} = 8\vec i + 6\vec j + 4\vec k\).
Suy ra \(\overrightarrow {AB} = (8;0;0);\overrightarrow {AC} = (8;6;0);\overrightarrow {A{C^\prime }} = (8;6;4)\).
\({\rm{V`i }}\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {A{C^\prime }} + \overrightarrow {A{D^\prime }} } \right) = \frac{1}{2}\left( {\overrightarrow {A{C^\prime }} + \overrightarrow {AD} + \overrightarrow {A{A^\prime }} } \right) = \frac{1}{2}(8\vec i + 6\vec j + 4\vec k + 6\vec j + 4\vec k) = 4\vec i + 6\vec j + 4\vec k\) \({\rm{n^e n }}\overrightarrow {AM} = (4;6;4).\)
Lời giải
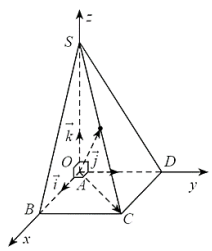
Ba vectơ đơn vị trên ba trục tọa độ lần lượt là \(\vec i,\vec j,\vec k\) với độ dài của \(\vec i,\vec j,\vec k\) lần lượt bằng \(\frac{1}{2}AB,\frac{1}{2}AD,\frac{1}{3}AS\)
b) Ta có: \(\overrightarrow {AB} = 2\vec i;\overrightarrow {AD} = 2\vec j;\overrightarrow {AS} = 3\vec k\).
Do đó \(\overrightarrow {AB} = (2;0;0),\overrightarrow {AD} = (0;2;0),\overrightarrow {AS} = (0;0;3)\).
Theo quy tắc hình bình hành, ta có \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} = 2\vec i + 2\vec j\).
Vì \({\rm{M}}\) là trung diếm của SC nên \(\overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AC} + \overrightarrow {AS} ) = \frac{1}{2}(2\vec i + 2\vec j + 3\vec k) = \vec i + \vec j + \frac{3}{2}\vec k\).
Do đó \(\overrightarrow {AM} = \left( {1;1;\frac{3}{2}} \right)\).