6 bài tập Tìm GTLN – GTNN của hàm số y = f(x) trên đoạn (có lời giải)

Ta có: f '(x) = 4x³ − 16x;

           f '(x) = 0 ⇔ x = 0 hoặc x = 2 hoặc x = −2 (loại vì không thuộc [−1; 3]);    

           f (−1) = 2; f (0) = 9; f (2) = −7; f (3) = 18.

Vậy \[\mathop {\max }\limits_{\left[ { - 1;3} \right]} \] f (x) = f (3) = 18 và \[\mathop {\min }\limits_{\left[ { - 1;3} \right]} \] f (x) = f (2) = −7.

Xét \(f(x) = 2{x^3} - 9{x^2} + 12x + 1\) trên đoạn [0 ; 3]; \({f^\prime }(x) = 6{x^2} - 18x + 12 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x = 1}\end{array}} \right.\)

Bảng biến thiên:

Từ bảng biến thiên, ta thấy \({\min _{[0,3]}}f(x) = f(0) = 1\) và \({\max _{[0,3]}}f(x) = f(3) = 10\)

Xét \(h(x) = x\sqrt {2 - {x^2}} \)

Tập xác định: \(D = [ - \sqrt 2 ;\sqrt 2 ]\); \({h^\prime }(x) = \sqrt {2 - {x^2}} - \frac{{{x^2}}}{{\sqrt {2 - {x^2}} }}\)

Tập xác định mới: \({D_1} = ( - \sqrt 2 ;\sqrt 2 )\); \({h^\prime }(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = - 1}\end{array}} \right.\)

Bảng biến thiên:

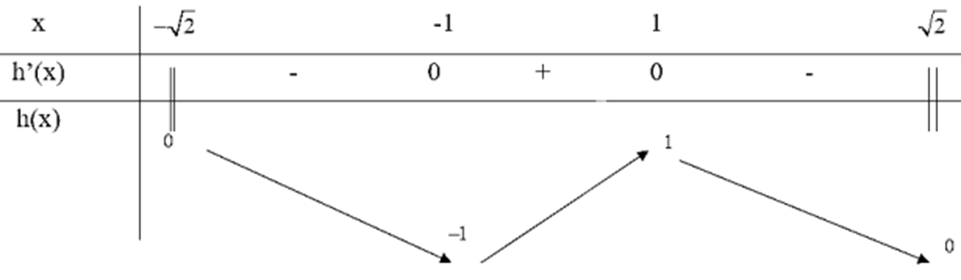
Từ bảng biến thiên, ta thấy \({\min _D}f(x) = f( - 1) = - 1\) và \({\max _D}f(x) = f(1) = 1\)

Ta có: \({y^\prime } = 6{x^2} - 6x + 5 = 6\left( {{x^2} - x + \frac{5}{6}} \right) = 6{\left( {x - \frac{1}{2}} \right)^2} + \frac{7}{2} > 0\forall x \in [0;2]\)

Do đó, hàm số \(y = 2{x^3} - 3{x^2} + 5x + 2\) đồng biến trên [0 ; 2].

Ta có: \(y(0) = 2;y(2) = {2.2^3} - {3.2^2} + 5.2 + 2 = 16\)

Do đó, \({\max _{[0;2]}}y = y(2) = 16,{\min _{[0,2]}}y = y(0) = 2\)

Ta có: \({y^\prime } = {e^{ - x}} - (x + 1){e^{ - x}} = {e^{ - x}}(1 - x - 1) = - x \cdot {e^{ - x}}\)

\({y^\prime } = 0 \Leftrightarrow - x.{e^{ - x}} = 0 \Leftrightarrow x = 0\) (thỏa mãn \(x \in [ - 1;1]\) )

\(y( - 1) = 0;y(0) = 1;y(1) = \frac{2}{2}\) Do đó, \({\max _{[ - 1;1]}}y = y(0) = 1,{\min _{[ - 1;1]}}y = y( - 1) = 0\)